题目内容
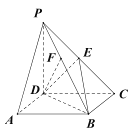
【题目】如图,在正四棱锥![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,
上,![]() .
.
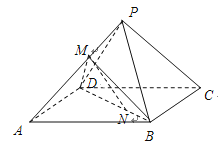
(1)若![]() ,求证:
,求证:![]() ⊥
⊥![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题由于图形是正四棱锥,因此设AC、BD交点为O,则以OA为x轴正方向,以OB为y轴正方向,OP为z轴正方向建立空间直角坐标系,可用空间向量法解决问题.(1)只要证明![]() =0即可证明垂直;(2)设
=0即可证明垂直;(2)设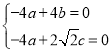 =λ
=λ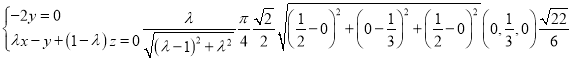 ,得M(λ,0,1-λ),然后求出平面MBD的法向量
,得M(λ,0,1-λ),然后求出平面MBD的法向量![]() ,而平面ABD的法向量为
,而平面ABD的法向量为![]() ,利用法向量夹角与二面角相等或互补可求得
,利用法向量夹角与二面角相等或互补可求得![]() .
.
试题解析: (1)连结AC、BD交于点O,以OA为x轴正方向,以OB为y轴正方向,OP为z轴正方向建立空间直角坐标系.
因为PA=AB=![]() ,
,
则A(1,0,0),B(0,1,0),D(0,-1,0),P(0,0,1).
由![]() =
=![]() ,得N
,得N![]() ,
,
由![]() =
=![]() ,得M
,得M![]() ,
,
所以![]() ,
,![]() =(-1,-1,0).
=(-1,-1,0).
因为![]() =0,所以MN⊥AD
=0,所以MN⊥AD
(2) 解:因为M在PA上,可设![]() =λ
=λ![]() ,得M(λ,0,1-λ).
,得M(λ,0,1-λ).
所以![]() =(λ,-1,1-λ),
=(λ,-1,1-λ),![]() =(0,-2,0).
=(0,-2,0).
设平面MBD的法向量![]() =(x,y,z),
=(x,y,z),
由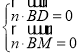 ,得
,得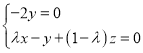
其中一组解为x=λ-1,y=0,z=λ,所以可取![]() =(λ-1,0,λ).
=(λ-1,0,λ).
因为平面ABD的法向量为![]() =(0,0,1),
=(0,0,1),
所以cos![]() =
=![]() ,即
,即![]() =
=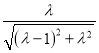 ,解得λ=
,解得λ=![]() ,
,
从而M![]() ,N
,N![]() ,
,
所以MN=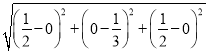 =
=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目