题目内容
在球面上有四个点P、A、B、C,如果PA、PB、PC两两互相垂直,且PA=a,PB=b,PC=c,那么这个球的体积是_________.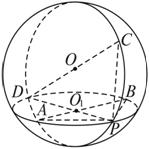
思路解析:求球的体积的关键是确定球的半径.把三棱锥P—ABC“补形”成棱长分别为a、b、c的长方体,显然该长方体仍内接于原来的球,且球的直径等于长方体的对角线,即2R=l,其中l2=a2+b2+c2.
于是R=![]() ,V球=
,V球=![]() .
.
答案: ![]()
方法归纳 本题的求解利用了“构造法”,也可以说是一种特殊的“补形法”.由三侧棱两两互相垂直,可想到长方体的一个角,因而可构造长方体进行解题.
又如,在三棱锥的四个面中,直角三角形最多可有多少个?便可以构造长方体ABCD—A1B1C1D1,并考察三棱锥A1—BB1C,易知该三棱锥的每个面都是直角三角形,故最多有4个直角三角形,即每个面所在的三角形均是直角三角形.

练习册系列答案
相关题目