题目内容
已知椭圆与双曲线| x2 | 3 |
分析:先把曲线的标准标准方程,其渐近线方程是
-y2=0,整理后就得到双曲线的渐近线方程.利用椭圆与双曲线有共同的焦点F1(-2,0),F2(2,0),设出椭圆方程,再利用点P(2,3)适合椭圆方程,就可求出椭圆的方程.
| x2 |
| 3 |
解答:解:双曲线的标准形式为
-y2=1,
其渐近线方程是
-y2=0,
整理得双曲线的渐近线为:x±
y=0.
由共同的焦点F1(-2,0),F2(2,0),可设椭圆方程为
+
=1,
点P(2,3)在椭圆上,
,
∴a2=16,b2=12,
所以椭圆方程为:
+
=1.
| x2 |
| 3 |
其渐近线方程是
| x2 |
| 3 |
整理得双曲线的渐近线为:x±
| 3 |
由共同的焦点F1(-2,0),F2(2,0),可设椭圆方程为
| y2 |
| a2 |
| x2 |
| b2 |
点P(2,3)在椭圆上,
|
∴a2=16,b2=12,
所以椭圆方程为:
| y2 |
| 16 |
| x2 |
| 12 |
点评:本题考查本题考查双曲线的标准方程,以及椭圆的标准方程的求法,令标准方程中的“1”为“0”即可求出渐近线方程.在求双曲线与椭圆的标准方程时,一定要先分析焦点所在位置,再设方程,避免出错.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. =2
=2 ,求△AOB的面积.
,求△AOB的面积. 与双曲线
与双曲线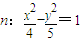 有两个公共点,且椭圆m与双曲线n的离心率之和为2.
有两个公共点,且椭圆m与双曲线n的离心率之和为2.