题目内容
已知椭圆 与双曲线
与双曲线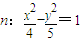 有两个公共点,且椭圆m与双曲线n的离心率之和为2.
有两个公共点,且椭圆m与双曲线n的离心率之和为2.(1)求椭圆m的方程;
(2)过椭圆m上的动点P作互相垂直的两条直线l1,l2,l1与圆O:x2+y2=a2+b2相交于点A,C,l2与圆x∈[2,6]相交于点B,D,求四边形ABCD的面积的最小值.

【答案】分析:(1)由题设条件得a=2,再由双曲线n的离心率为 ,知椭圆m的离心率
,知椭圆m的离心率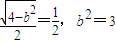 .由此能求出椭圆m的方程.
.由此能求出椭圆m的方程.
(2)圆O的方程为x2+y2=7.若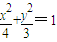 ,则
,则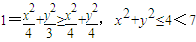 ,椭圆m落在圆O内.设点P(x,y)到直线l1,l2的距离分别为d1,d2,则
,椭圆m落在圆O内.设点P(x,y)到直线l1,l2的距离分别为d1,d2,则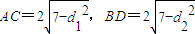 .由此入手能够求出四边形ABCD的面积的最小值.
.由此入手能够求出四边形ABCD的面积的最小值.
解答: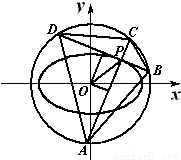 解:(1)若a>2,则椭圆m与双曲线n有四个公共点;
解:(1)若a>2,则椭圆m与双曲线n有四个公共点;
若0<a<2,则椭圆m与双曲线n没有公共点;
若a=2,则椭圆m与双曲线n有公共点(±2,0).
由题意,可得a=2.…(3分)
又双曲线n的离心率为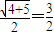 ,
,
则椭圆m的离心率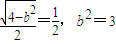 .
.
所以椭圆m的方程为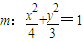 .…(6分)
.…(6分)
(2)圆O的方程为x2+y2=7.
若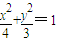 ,
,
则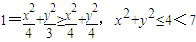 ,
,
即椭圆m落在圆O内.
如图,设点P(x,y)到直线l1,l2的距离分别为d1,d2,
则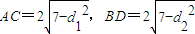 ,…(7分)
,…(7分)
由l1⊥l2,得d12+d22=OP2=x2+y2.
四边形ABCD的面积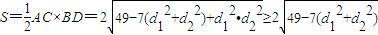 …(9分)
…(9分)
由点P(x,y)在椭圆m上,
则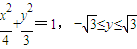 .
.
又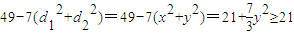 ,得
,得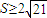 .…(11分)
.…(11分)
当且仅当d1d2=0且y=0,
即P的坐标为(-2,0),
直线l1,l2的方程为y=0,
x=-2或P的坐标为(2,0),
直线l1,l2的方程为y=0,x=2时,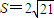 .…(13分)
.…(13分)
所以四边形ABCD的面积的最小值为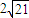 .…(14分)
.…(14分)
点评:本题考查和椭圆的关系的综合运用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.
 ,知椭圆m的离心率
,知椭圆m的离心率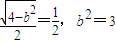 .由此能求出椭圆m的方程.
.由此能求出椭圆m的方程.(2)圆O的方程为x2+y2=7.若
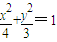 ,则
,则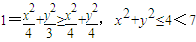 ,椭圆m落在圆O内.设点P(x,y)到直线l1,l2的距离分别为d1,d2,则
,椭圆m落在圆O内.设点P(x,y)到直线l1,l2的距离分别为d1,d2,则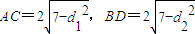 .由此入手能够求出四边形ABCD的面积的最小值.
.由此入手能够求出四边形ABCD的面积的最小值.解答:
 解:(1)若a>2,则椭圆m与双曲线n有四个公共点;
解:(1)若a>2,则椭圆m与双曲线n有四个公共点;若0<a<2,则椭圆m与双曲线n没有公共点;
若a=2,则椭圆m与双曲线n有公共点(±2,0).
由题意,可得a=2.…(3分)
又双曲线n的离心率为
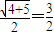 ,
,则椭圆m的离心率
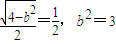 .
.所以椭圆m的方程为
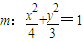 .…(6分)
.…(6分)(2)圆O的方程为x2+y2=7.
若
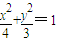 ,
,则
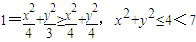 ,
,即椭圆m落在圆O内.
如图,设点P(x,y)到直线l1,l2的距离分别为d1,d2,
则
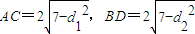 ,…(7分)
,…(7分)由l1⊥l2,得d12+d22=OP2=x2+y2.
四边形ABCD的面积
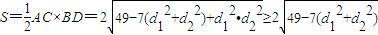 …(9分)
…(9分)由点P(x,y)在椭圆m上,
则
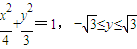 .
.又
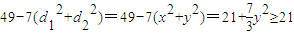 ,得
,得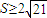 .…(11分)
.…(11分)当且仅当d1d2=0且y=0,
即P的坐标为(-2,0),
直线l1,l2的方程为y=0,
x=-2或P的坐标为(2,0),
直线l1,l2的方程为y=0,x=2时,
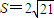 .…(13分)
.…(13分)所以四边形ABCD的面积的最小值为
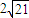 .…(14分)
.…(14分)点评:本题考查和椭圆的关系的综合运用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目





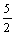
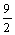
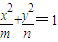 与双曲线
与双曲线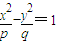 (m,n,p,q∈R+)有共同的焦点F1,F2,P是两曲线的一个公共交点.则|PF1|•|PF2|的值是( )
(m,n,p,q∈R+)有共同的焦点F1,F2,P是两曲线的一个公共交点.则|PF1|•|PF2|的值是( )