题目内容
已知椭圆与双曲线x2-y2=1有相同的焦点,且离心率为 .
.(I)求椭圆的标准方程;
(II)过点P(0,1)的直线与该椭圆交于A、B两点,O为坐标原点,若
 =2
=2 ,求△AOB的面积.
,求△AOB的面积.
【答案】分析:(I)设椭圆方程为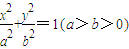 ,由椭圆与双曲线x2-y2=1有相同的焦点可得c值,由离心率可得a值,根据 平方关系可得b;
,由椭圆与双曲线x2-y2=1有相同的焦点可得c值,由离心率可得a值,根据 平方关系可得b;
(II)设A(x1,y1),B(x2,y2),由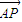 =2
=2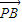 ,得
,得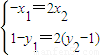 ,设直线方程为y=kx+1,代入椭圆方程整理,得(2k2+1)x2+4kx-2=0,△AOB的面积S=S△OAP+S△OBP=
,设直线方程为y=kx+1,代入椭圆方程整理,得(2k2+1)x2+4kx-2=0,△AOB的面积S=S△OAP+S△OBP=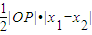 ,根据韦达定理及弦长公式即可求得答案;
,根据韦达定理及弦长公式即可求得答案;
解答:解:(I)设椭圆方程为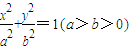 ,
,
因为椭圆与双曲线有相同焦点,
所以c=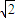 ,再由e=
,再由e=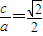 可得a=2,∴b2=a2-c2=2,
可得a=2,∴b2=a2-c2=2,
故所求方程为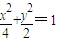 ;
;
(II)设A(x1,y1),B(x2,y2),
由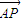 =2
=2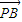 ,得
,得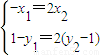 ,
,
设直线方程为y=kx+1,代入椭圆方程整理,得(2k2+1)x2+4kx-2=0,
解得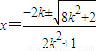 ,
,
若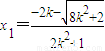 ,
,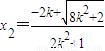 ,
,
则-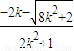 =2
=2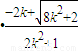 ,
,
解得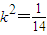 ,
,
又△AOB的面积S=S△OAP+S△OBP=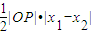 =
=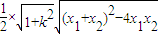 =
=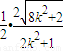 =
=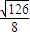 ,
,
故所求△AOB的面积是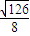 .
.
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查平面向量的基本运算,解决(II)问的关键是恰当表示出△AOB的面积.
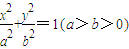 ,由椭圆与双曲线x2-y2=1有相同的焦点可得c值,由离心率可得a值,根据 平方关系可得b;
,由椭圆与双曲线x2-y2=1有相同的焦点可得c值,由离心率可得a值,根据 平方关系可得b;(II)设A(x1,y1),B(x2,y2),由
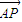 =2
=2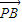 ,得
,得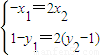 ,设直线方程为y=kx+1,代入椭圆方程整理,得(2k2+1)x2+4kx-2=0,△AOB的面积S=S△OAP+S△OBP=
,设直线方程为y=kx+1,代入椭圆方程整理,得(2k2+1)x2+4kx-2=0,△AOB的面积S=S△OAP+S△OBP=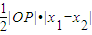 ,根据韦达定理及弦长公式即可求得答案;
,根据韦达定理及弦长公式即可求得答案;解答:解:(I)设椭圆方程为
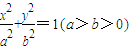 ,
,因为椭圆与双曲线有相同焦点,
所以c=
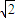 ,再由e=
,再由e=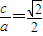 可得a=2,∴b2=a2-c2=2,
可得a=2,∴b2=a2-c2=2,故所求方程为
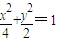 ;
;(II)设A(x1,y1),B(x2,y2),
由
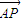 =2
=2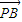 ,得
,得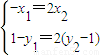 ,
,设直线方程为y=kx+1,代入椭圆方程整理,得(2k2+1)x2+4kx-2=0,
解得
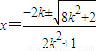 ,
,若
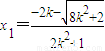 ,
,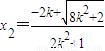 ,
,则-
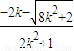 =2
=2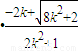 ,
,解得
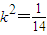 ,
,又△AOB的面积S=S△OAP+S△OBP=
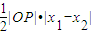 =
=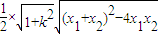 =
=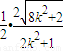 =
=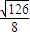 ,
,故所求△AOB的面积是
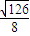 .
.点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查平面向量的基本运算,解决(II)问的关键是恰当表示出△AOB的面积.

练习册系列答案
相关题目
 与双曲线
与双曲线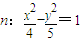 有两个公共点,且椭圆m与双曲线n的离心率之和为2.
有两个公共点,且椭圆m与双曲线n的离心率之和为2.