题目内容
(12分)如图,正四棱锥P![]() ABCD的底面边长与侧棱长都是2,点O为底面ABCD的中心,M为PC的中点.
ABCD的底面边长与侧棱长都是2,点O为底面ABCD的中心,M为PC的中点.
(Ⅰ)求异面直线BM和AD所成角的大小;
(Ⅱ)求二面角M![]() PB
PB![]() D的余弦值.
D的余弦值.

解析:(Ⅰ)连接![]() ,以
,以![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴
轴
建立空间直角坐标系. …………………………………(2分)
![]() 正四棱锥的底面边长和侧棱长都是2,
正四棱锥的底面边长和侧棱长都是2,
![]() .
.
![]() .
.
![]()
![]() 为
为![]() 的中点.
的中点.
![]() …………(4分)
…………(4分)
![]() .
.

![]()
![]() 即异面直线
即异面直线![]() 和
和![]() 所成的角为
所成的角为![]() ………(6分)
………(6分)
(Ⅱ)![]() .
.
![]() 是平面
是平面![]() 的一个法向量. ……………………………(8分)
的一个法向量. ……………………………(8分)
由(Ⅰ)得![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则由![]() ,得
,得 .
.
![]() ,不妨设
,不妨设![]() ,
,
得平面![]() 的一个法向量为
的一个法向量为![]() . ………………(10分)
. ………………(10分)
 .
.
![]() 二面角
二面角![]() 小于
小于![]() ,
,

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
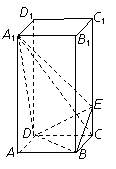
(本小题满分12分)
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上,且![]() 平面BED
平面BED
(Ⅰ)证明; C1E=3EC
|
(本小题满分12分)
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上,且![]() 平面BED
平面BED
(Ⅰ)证明; C1E=3EC
|

 正方形,
正方形, 为底面
为底面 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.

 为
为 中点,求证:
中点,求证: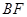 ∥平面PAC;
∥平面PAC;