题目内容
(本小题满分12分)已知函数 (其中
(其中 )
)
(I)求函数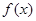 的值域;
的值域;
(II)若对任意的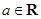 ,函数
,函数 ,
, 的图象与直线
的图象与直线 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定 的值(不必证明),并求函数
的值(不必证明),并求函数 的单调增区间.
的单调增区间.
 (其中
(其中 )
)(I)求函数
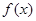 的值域;
的值域;(II)若对任意的
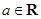 ,函数
,函数 ,
, 的图象与直线
的图象与直线 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定 的值(不必证明),并求函数
的值(不必证明),并求函数 的单调增区间.
的单调增区间.(I)函数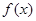 的值域为[-3,1]
的值域为[-3,1]
(II)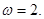
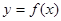 的单调增区间为[
的单调增区间为[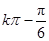 ,
,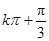 ]
]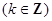 .
.
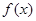 的值域为[-3,1]
的值域为[-3,1](II)
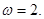
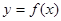 的单调增区间为[
的单调增区间为[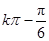 ,
,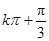 ]
] .
.解: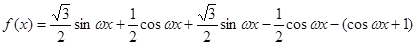
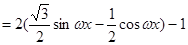
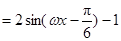 5分
5分
由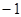 ≤
≤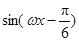 ≤,得
≤,得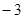 ≤2
≤2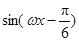
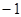 ≤1.
≤1.
可知函数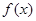 的值域为[-3,1]. 7分
的值域为[-3,1]. 7分
(Ⅱ)解:由题设条件及三角函数图象和性质可知,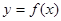 的周期为
的周期为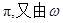 >0,得
>0,得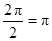 ,即得
,即得

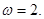 9分
9分
于是有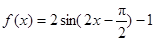 ,再由
,再由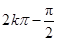 ≤
≤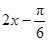 ≤
≤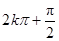
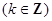 ,解得
,解得
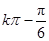 ≤x≤
≤x≤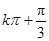
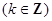 .
.
所以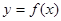 的单调增区间为[
的单调增区间为[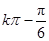 ,
,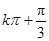 ]
]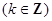 . 12分
. 12分
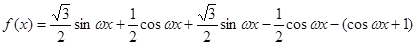
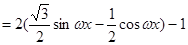
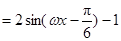 5分
5分由
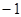 ≤
≤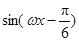 ≤,得
≤,得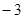 ≤2
≤2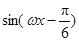
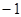 ≤1.
≤1.可知函数
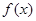 的值域为[-3,1]. 7分
的值域为[-3,1]. 7分(Ⅱ)解:由题设条件及三角函数图象和性质可知,
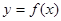 的周期为
的周期为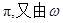 >0,得
>0,得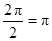 ,即得
,即得
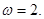 9分
9分于是有
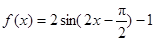 ,再由
,再由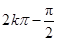 ≤
≤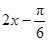 ≤
≤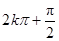
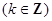 ,解得
,解得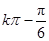 ≤x≤
≤x≤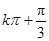
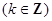 .
.所以
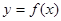 的单调增区间为[
的单调增区间为[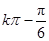 ,
,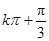 ]
]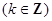 . 12分
. 12分
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
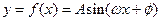 ,(
,(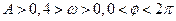 )的一段图象如图,
)的一段图象如图,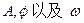 的值
的值 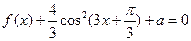 有解,求
有解,求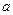 的取值范围
的取值范围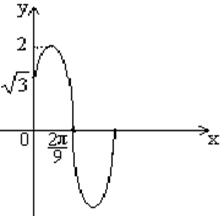
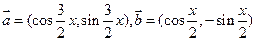 若
若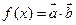 .
.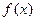 的最小正周期;
的最小正周期;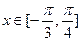 求函数
求函数 ,
, ,且
,且 。
。 的表达式化为
的表达式化为 的形式;
的形式; ,求函数
,求函数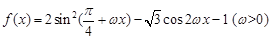 的最小正周期为
的最小正周期为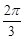
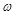 的值;
的值; 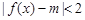 在
在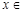
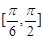 上恒成立,求实数
上恒成立,求实数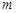 的取值范围.
的取值范围.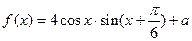 的最大值为2。
的最大值为2。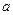 的值及
的值及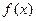 的最小正周期;
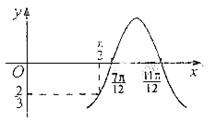
的最小正周期;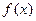 =Acos(
=Acos(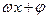 )的图象如图所示,
)的图象如图所示,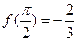 ,则
,则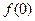 =( )
=( )


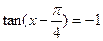 ,则
,则 的取值集合是__________
的取值集合是__________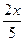 +cos
+cos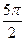 ;③函数f(x)的图象上相邻的两条对称轴之间的距离是
;③函数f(x)的图象上相邻的两条对称轴之间的距离是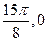 )是函数f(x)图象的一个对称中心.
)是函数f(x)图象的一个对称中心.