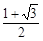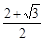题目内容
若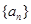 是等差数列,首项公差
是等差数列,首项公差 ,
,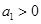 ,且
,且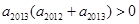 ,则使数列
,则使数列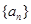 的前n项和
的前n项和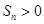 成立的最大自然数n是 ( )
成立的最大自然数n是 ( )
| A.4027 | B.4026 | C.4025 | D.4024 |
D
解析试题分析:对于首项大于零的递减的等差数列,由等差数列前n项和公式可判断结论.
根据题意可知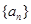 是等差数列,首项公差
是等差数列,首项公差 ,
,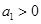 ,且
,且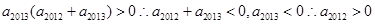 ,
,
可知,数列是递减的数列,同时可知则利用等差中项性质可知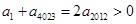 ,同理
,同理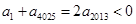 ,所以
,所以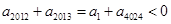 ,因此使数列
,因此使数列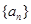 的前n项和
的前n项和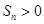 成立的最大自然数n是4024,因此选D.
成立的最大自然数n是4024,因此选D.
考点:等差数列以及性质的运用
点评:本题没有具体的数字运算,它考查的是等差数列的性质,有数列的等差中项,等差数列的前n项和,实际上这类问题比具体的数字运算要困难,对同学们来说有些抽象

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
一等差数列的前n项和为210,其中前4项的和为40,后4项的和为80,则n的值为( )
| A.12 | B.14 |
| C.16 | D.18 |
设Sn是等差数列{an}的前n项和,若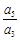 =
=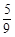 ,则
,则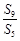 =( ).
=( ).
| A.1 | B.-1 | C.2 | D.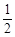 |
等差数列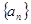 的前项
的前项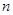 和为
和为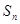 ,若
,若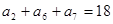 ,则
,则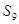 的值为( )
的值为( )
A.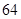 | B.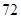 | C.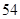 | D.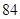 |
若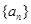 是等差数列,首项
是等差数列,首项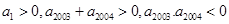 ,则使前n项和
,则使前n项和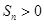 成立的最大自然数n是:( )
成立的最大自然数n是:( )
| A.4005 | B.4006 | C.4007 | D.4008 |
已知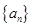 是等差数列,
是等差数列,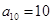 ,其前10项和
,其前10项和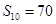 ,则其公差
,则其公差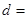 ( )
( )
A.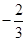 | B.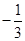 | C. | D.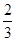 |
已知正项数列{ }中,al=1,a2=2,2
}中,al=1,a2=2,2 2=
2= 2+
2+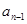 2 (n≥2),则a6等于
2 (n≥2),则a6等于
| A.16 | B.8 | C.2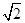 | D.4 |
已知等差数列 中,
中,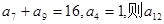 的值是( )
的值是( )
| A.15 | B.30 | C.31 | D.64 |
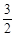 ,那么b=( ).
,那么b=( ).