题目内容
一等差数列的前n项和为210,其中前4项的和为40,后4项的和为80,则n的值为( )
| A.12 | B.14 |
| C.16 | D.18 |
B
解析试题分析:由a1+a2+a3+a4=40. an+an-1+an-2+an-3=80.
得4(a1+an)=120,所以a1+an=30.所以Sn=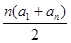 =
=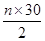 =210. n=14.∴选B.
=210. n=14.∴选B.
考点:等差数列的性质
点评:本题考查等差数列的性质,解题的关键是理解并会利用等差数列的性质序号的和相等项的和也相等求出首末两项的和,再利用等差数列的前n项和公式建立方程求出项数,本题是等差数列的基本题也是高考试卷上一个比较热的题,本题中考查的性质是等差数列中非常重要的一个性质,就好好理解掌握

练习册系列答案
相关题目
等差数列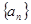 中,
中, 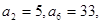 则
则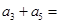 ( )
( )
A.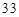 | B.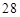 | C.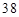 | D.52 |
在等差数列 中,若
中,若 ,则
,则 等于( )
等于( )
| A.3 | B.4 | C.5 | D.6 |
已知等差数列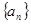 的前三项依次为
的前三项依次为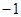 ,
, ,
,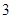 ,则此数列的通项公式为( )
,则此数列的通项公式为( )
A.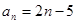 | B.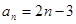 | C.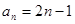 | D.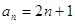 |
若数列{an}是公差为 的等差数列,它的前100项和为145,则a1+a3+a5+…+a99的值是
的等差数列,它的前100项和为145,则a1+a3+a5+…+a99的值是
| A.60 | B.72.5 | C.85 | D.120 |
已知数列 ,
, ,
,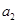 ,
, 成等差数列,
成等差数列,  ,
, ,
, ,
, ,
, 成等比数列,则
成等比数列,则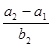 的值为( )
的值为( )
A. | B. | C. 或 或 | D. |
已知等差数列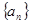 中,
中,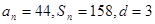 , 则n=( )
, 则n=( )
| A.4 | B.5 | C.6 | D.7 |
若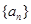 是等差数列,首项公差
是等差数列,首项公差 ,
,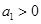 ,且
,且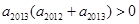 ,则使数列
,则使数列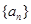 的前n项和
的前n项和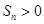 成立的最大自然数n是 ( )
成立的最大自然数n是 ( )
| A.4027 | B.4026 | C.4025 | D.4024 |
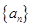 中,若a
中,若a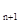 - a
- a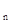
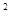 + a
+ a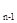 =0(n≥2),则S
=0(n≥2),则S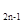 -4n=( )
-4n=( )