题目内容
三棱锥A-BCD中，AB=CD=2，AD=BC=
，AC=BD=
则三棱锥A-BCD的外接球的表面积为
| 5 |
| 7 |
8π
8π
．分析：三棱锥A-BCD的三条侧棱两两相等，所以把它扩展为长方体，它也外接于球，对角线的长为球的直径，然后解答即可．
解答：解：三棱锥A-BCD的三条侧棱两两相等，所以把它扩展为长方体，
它也外接于球，且此长方体的面对角线的长分别为：2，
，
体对角线的长为球的直径，d=
=2
∴它的外接球半径是
外接球的表面积是 4π(
)2=8π
故答案为：8π
它也外接于球，且此长方体的面对角线的长分别为：2，
| 5 |
| 7 |
体对角线的长为球的直径，d=
|
| 2 |
∴它的外接球半径是
| 2 |
外接球的表面积是 4π(
| 2 |
故答案为：8π
点评：本题考查球的体积和，球内接多面体及其度量，考查空间想象能力，计算能力，是基础题，解答的关键是构造球的内接长方体，利用体对角线的长为球的直径解决问题．
练习册系列答案
相关题目
如图，在三棱锥A-BCD中，E、F、G、H分别是边AB、BC、CD、DA的中点．
如图，在三棱锥A-BCD中，AD⊥平面ABC，∠BAC=120°，且AB=AC=AD=2，点E在BC上，且AE⊥AC．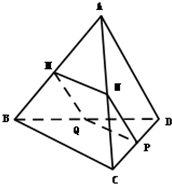
如图，在三棱锥A-BCD中，平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点，且MN=PQ．