题目内容
已知在三棱锥A-BCD中,M,N分别为AB,CD的中点 则下列结论正确的是( )
分析:取BC的中点E,并连接ME、NE,利用三角形的中位线定理可得ME=
AC,EN=
BD;又在△MNE中,有ME+EN>MN进而即可得出答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:如图所示,取BC的中点E,连接ME、EN,
解:如图所示,取BC的中点E,连接ME、EN,
在△ABC中,∵AM=MB,CE=EB,∴ME=
AC,
同理EN=
BD,
在△MEN中,∵ME+EN>MN,
∴
AC+
BD>MN,即MN<
(AC+BD).
故选D.
 解:如图所示,取BC的中点E,连接ME、EN,
解:如图所示,取BC的中点E,连接ME、EN,在△ABC中,∵AM=MB,CE=EB,∴ME=
| 1 |
| 2 |
同理EN=
| 1 |
| 2 |
在△MEN中,∵ME+EN>MN,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选D.
点评:利用三角形中的三边大小关系和三角形的中位线定理是解决问题的关键.

练习册系列答案
相关题目
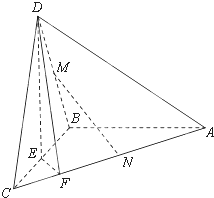 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC.
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC. 已知在三棱锥P-ABC中,PA⊥面ABC,AC⊥BC,且PA=AC=BC=1,点E是PC的中点,作EF⊥PB交PB于点F.
已知在三棱锥P-ABC中,PA⊥面ABC,AC⊥BC,且PA=AC=BC=1,点E是PC的中点,作EF⊥PB交PB于点F.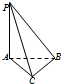 已知如图在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,PA=AC=BC=1,若三棱锥P-ABC的四个顶点都在某一个球面上,则该球的表面积为( )
已知如图在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,PA=AC=BC=1,若三棱锥P-ABC的四个顶点都在某一个球面上,则该球的表面积为( )