题目内容
1.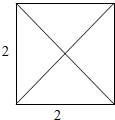 已知四棱锥的底面是边长为2的正方形,侧棱长都等于$\sqrt{11}$,其俯视图如图所示.
已知四棱锥的底面是边长为2的正方形,侧棱长都等于$\sqrt{11}$,其俯视图如图所示.(I)作出该四棱锥的侧视图,注明各线段的长,并计算该侧视图的面积;
(Ⅱ)求这个四棱锥的体积.
分析 (Ⅰ)由已知得到四棱锥S-ABCD中SA=SB=SC=SD=$\sqrt{11}$,AB=BC=CD=DA=2,取AD中点E,取BC中点F,AC∩BD=O,连结SE、SF、SO,则$SE=SF=\sqrt{11-1}$=$\sqrt{10}$,SO=$\sqrt{10-1}$=3,从而得到该四棱锥的侧视图是腰为$\sqrt{10}$,底为2,高为3的等腰三角形,由此能求出侧视图的面积.
(Ⅱ)先求出这个四棱锥的底面积和高,由此能求出这个四棱锥的体积.
解答 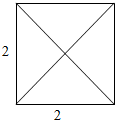 解:(Ⅰ)∵四棱锥的底面是边长为2的正方形,侧棱长都等于$\sqrt{11}$,
解:(Ⅰ)∵四棱锥的底面是边长为2的正方形,侧棱长都等于$\sqrt{11}$,
其俯视图如右图,
∴该四棱锥为如图所示的四棱锥S-ABCD,
其中SA=SB=SC=SD=$\sqrt{11}$,AB=BC=CD=DA=2,
取AD中点E,取BC中点F,AC∩BD=O,
连结SE、SF、SO,
则$SE=SF=\sqrt{11-1}$=$\sqrt{10}$,SO=$\sqrt{10-1}$=3,
∴该四棱锥的侧视图是腰为$\sqrt{10}$,底为2,高为3的等腰三角形,如下图:
该侧视图的面积S=$\frac{1}{2}×2×3$=3.
(Ⅱ)∵这个四棱锥的底面积SABCD=2×2=4,高SO=3,
∴这个四棱锥的体积:
V=$\frac{1}{3}×{S}_{ABCD}×SO$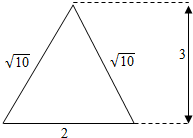
=$\frac{1}{3}×4×3$
=4.
点评 本题考查四棱锥的侧视图的作法及侧视图的面积的求法,考查四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
10.已知△ABC的周长为18,|AB|=8且A(-4,0),B(4,0),|CA|<|CB|,则C点的轨迹方程为( )
| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(y≠0) | B. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(y≠0,x<0) | ||
| C. | $\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{9}$=1(y≠0) | D. | $\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{9}$=1(y≠0,x<0) |