题目内容
12.已知椭圆的对称轴为坐标轴,离心率e=$\frac{\sqrt{3}}{2}$,短轴长为6,求椭圆的标准方程.分析 当焦点在x轴上时,设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),可得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{2b=6}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解出即可得出;当焦点在y轴上时,同理可得椭圆的标准方程.
解答 解:当焦点在x轴上时,设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),可得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{2b=6}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=6,b=3,
可得椭圆的标准方程为$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{9}$=1.
当焦点在y轴上时,同理可得椭圆的标准方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{36}$=1.
点评 本题考查了椭圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列函数中,是奇函数且在区间(-∞,0)上为增函数的是( )
| A. | y=x3+3 | B. | y=x3 | C. | y=x-1 | D. | y=ex |
7.已知椭圆的方程为$\frac{{x}^{2}}{49}$+$\frac{{y}^{2}}{25}$=1,则该椭圆的焦点坐标为( )
| A. | (0,-5),(0,5) | B. | (0,-7),(0,7) | C. | (-2$\sqrt{6}$,0),(2$\sqrt{6}$,0) | D. | (0,-2$\sqrt{6}$),(0,2$\sqrt{6}$) |
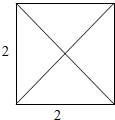 已知四棱锥的底面是边长为2的正方形,侧棱长都等于$\sqrt{11}$,其俯视图如图所示.
已知四棱锥的底面是边长为2的正方形,侧棱长都等于$\sqrt{11}$,其俯视图如图所示.