题目内容
已知集合A={x|2-a≤x≤2+a}，B={x|x2-5x+4≥0}．
（1）当a=3时，求A∩B；
（2）若a＞0，且A∩B=Φ，求实数a的取值范围．
解：（1）当a=3时，A={-1≤x≤5}，B={x≤1或x≥4}
∴A∩B={-1≤x≤1或4≤x≤5}
（2）∵A∩B=∅，A={x|2-a≤x≤2+a}（a＞0），B={x≤1或x≥4}
∴
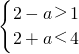
∴a＜1
∵a＞0
∴0＜a＜1
分析：（1）当a=3时，我们先分别化简集合A，B，再求A∩B；
（2）A∩B=∅，也就是，集合A，B没有公共元素，这样，就可以建立不等关系，从而可求实数a的取值范围．
点评：解答集合之间的关系的关键是理解集合的运算，建立不等关系，属于基础题．
∴A∩B={-1≤x≤1或4≤x≤5}
（2）∵A∩B=∅，A={x|2-a≤x≤2+a}（a＞0），B={x≤1或x≥4}
∴
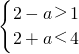
∴a＜1
∵a＞0
∴0＜a＜1
分析：（1）当a=3时，我们先分别化简集合A，B，再求A∩B；
（2）A∩B=∅，也就是，集合A，B没有公共元素，这样，就可以建立不等关系，从而可求实数a的取值范围．
点评：解答集合之间的关系的关键是理解集合的运算，建立不等关系，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目