题目内容
已知一动圆P(圆心为P)经过定点Q(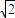 ,0),并且与定圆C:
,0),并且与定圆C: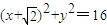 (圆心为C)相切.
(圆心为C)相切.(1)求动圆圆心P的轨迹方程;
(2)若斜率为k的直线l经过圆x2+y2-2x-2y=0的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得
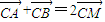 ?如果存在,求出k的值;如果不存在,请说明理由.
?如果存在,求出k的值;如果不存在,请说明理由.
【答案】分析:(1)设P(x,y),动圆半径为r,则|PQ|=r.因为点Q在圆C的内部,所以动圆P与定圆C内切,所以|PC|=4-r.
所以|PC|+|PQ|=4>|CQ|=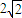 ,由此能够求出动圆圆心P的轨迹方程.
,由此能够求出动圆圆心P的轨迹方程.
(2)假设存在常数k,使得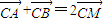 ,即
,即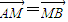 ,所以M为AB的中点.圆方程可化为(x-1)2+(y-1)2=2,所以圆心M为(1,1).直线l的方程为y-1=k(x-1).由
,所以M为AB的中点.圆方程可化为(x-1)2+(y-1)2=2,所以圆心M为(1,1).直线l的方程为y-1=k(x-1).由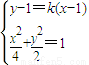 ,得(1+2k2)x2+(4k-4k2)x+(2k2-4k-2)=0.因为点M(1,1)在椭圆
,得(1+2k2)x2+(4k-4k2)x+(2k2-4k-2)=0.因为点M(1,1)在椭圆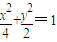 的内部,所以恒有△>0.由此能够推导出存在常数k=-
的内部,所以恒有△>0.由此能够推导出存在常数k=- ,使得
,使得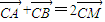 .
.
解答:(1)解:设P(x,y),动圆半径为r,则|PQ|=r.
因为点Q在圆C的内部,所以动圆P与定圆C内切,
所以|PC|=4-r.
所以|PC|+|PQ|=4>|CQ|=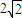 ,
,
根据椭圆的定义,动圆圆心P的轨迹是以C、Q为焦点的椭圆.
因为椭圆的中心在原点,焦点在x轴上,
故可设椭圆方程为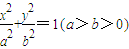 .
.
由2a=4,2c=2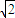 ,得a=2,c=
,得a=2,c=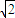 ,b=
,b=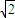 ,
,
所以椭圆方程为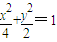 .
.
所以动圆圆心P的轨迹方程为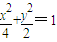 .
.
(2)解:假设存在常数k,使得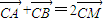 ,
,
即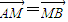 ,所以M为AB的中点.
,所以M为AB的中点.
圆方程可化为(x-1)2+(y-1)2=2,
所以圆心M为(1,1).
因为直线l经过点M,
所以直线l的方程为y-1=k(x-1).
由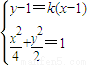 ,
,
消去y得(1+2k2)x2+(4k-4k2)x+(2k2-4k-2)=0.
因为点M(1,1)在椭圆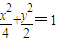 的内部,
的内部,
所以恒有△>0.
设A(x1,y1),B(x2,y2),
则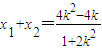 .
.
因为M为AB的中点,
所以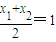 ,
,
即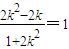 ,
,
解得k=- .
.
所以存在常数k=- ,
,
使得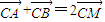 .
.
点评:本题通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.综合性强,难度大,容易出错.
所以|PC|+|PQ|=4>|CQ|=
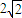 ,由此能够求出动圆圆心P的轨迹方程.
,由此能够求出动圆圆心P的轨迹方程.(2)假设存在常数k,使得
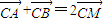 ,即
,即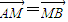 ,所以M为AB的中点.圆方程可化为(x-1)2+(y-1)2=2,所以圆心M为(1,1).直线l的方程为y-1=k(x-1).由
,所以M为AB的中点.圆方程可化为(x-1)2+(y-1)2=2,所以圆心M为(1,1).直线l的方程为y-1=k(x-1).由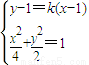 ,得(1+2k2)x2+(4k-4k2)x+(2k2-4k-2)=0.因为点M(1,1)在椭圆
,得(1+2k2)x2+(4k-4k2)x+(2k2-4k-2)=0.因为点M(1,1)在椭圆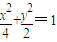 的内部,所以恒有△>0.由此能够推导出存在常数k=-
的内部,所以恒有△>0.由此能够推导出存在常数k=- ,使得
,使得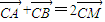 .
.解答:(1)解:设P(x,y),动圆半径为r,则|PQ|=r.
因为点Q在圆C的内部,所以动圆P与定圆C内切,
所以|PC|=4-r.
所以|PC|+|PQ|=4>|CQ|=
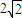 ,
,根据椭圆的定义,动圆圆心P的轨迹是以C、Q为焦点的椭圆.
因为椭圆的中心在原点,焦点在x轴上,
故可设椭圆方程为
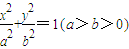 .
.由2a=4,2c=2
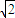 ,得a=2,c=
,得a=2,c=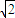 ,b=
,b=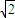 ,
,所以椭圆方程为
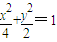 .
.所以动圆圆心P的轨迹方程为
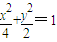 .
.(2)解:假设存在常数k,使得
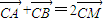 ,
,即
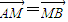 ,所以M为AB的中点.
,所以M为AB的中点.圆方程可化为(x-1)2+(y-1)2=2,
所以圆心M为(1,1).
因为直线l经过点M,
所以直线l的方程为y-1=k(x-1).
由
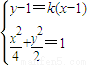 ,
,消去y得(1+2k2)x2+(4k-4k2)x+(2k2-4k-2)=0.
因为点M(1,1)在椭圆
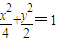 的内部,
的内部,所以恒有△>0.
设A(x1,y1),B(x2,y2),
则
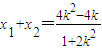 .
.因为M为AB的中点,
所以
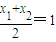 ,
,即
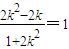 ,
,解得k=-
 .
.所以存在常数k=-
 ,
,使得
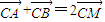 .
.点评:本题通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.综合性强,难度大,容易出错.

练习册系列答案
相关题目
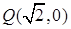 ,并且与定圆
,并且与定圆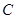 :
: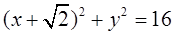 (圆心为C)相切.
(圆心为C)相切.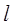 经过圆
经过圆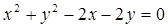 的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得
的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得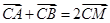 ?如果存在,求出
?如果存在,求出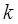 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.