题目内容
已知函数f(x)=x2+alnx.
(1)当a=-2e时,求函数f(x)的单调区间和极值.
(2)若函数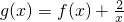 在[1,4]上是减函数,求实数a的取值范围.
在[1,4]上是减函数,求实数a的取值范围.
解:(1)函数f(x)的定义域为(0,+∞).
当a=-2e时,f′(x)=2x-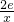 =
= (2分),
(2分),
当x变化时,f'(x),f(x)的变化情况如下:
∴f(x)的单调递减区间是(0, );单调递增区间是(
);单调递增区间是( ,+∞).
,+∞).
极小值是f( )=0.(6分)
)=0.(6分)
(2)由g(x)=x2+alnx+ ,得g′(x)=2x+
,得g′(x)=2x+ -
- (8分)
(8分)
又函数g(x)=x2+alnx+ 为[1,4]上的单调减函数.
为[1,4]上的单调减函数.
则g'(x)≤0在[1,4]上恒成立,
所以不等式2x+ -
- ≤0在[1,4]上恒成立,
≤0在[1,4]上恒成立,
即a≤ -2x2在[1,4]上恒成立. (10分)
-2x2在[1,4]上恒成立. (10分)
设φ(x)= -2x2,显然?(x)在[1,4]上为减函数,
-2x2,显然?(x)在[1,4]上为减函数,
所以?(x)的最小值为?(4)=-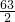 .
.
∴a的取值范围是a≤-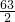 .(12分)
.(12分)
分析:(1)a=-2e时,f′(x)=2x-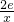 =
= ,利用x变化时,f'(x),f(x)的变化情况可求函数f(x)的单调区间和极值;
,利用x变化时,f'(x),f(x)的变化情况可求函数f(x)的单调区间和极值;
(2)由g(x)=x2+alnx+ ,得g′(x)=2x+
,得g′(x)=2x+ -
- ,由g'(x)≤0在[1,4]上恒成立,可得a≤
,由g'(x)≤0在[1,4]上恒成立,可得a≤ -2x2在[1,4]上恒成立.构造函数φ(x)=
-2x2在[1,4]上恒成立.构造函数φ(x)= -2x2,求其最小值即可.
-2x2,求其最小值即可.
点评:本题考查利用倒数研究函数的单调性,着重考查函数在某点取得极值的条件,考查闭区间上的恒成立问题,突出转化思想与构造函数的思想的运用,属于难题.
当a=-2e时,f′(x)=2x-
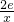 =
= (2分),
(2分),当x变化时,f'(x),f(x)的变化情况如下:
| x | 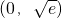 |  | 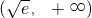 |
| f'(x) | - | 0 | + |
| f(x) | 极小值 |
 );单调递增区间是(
);单调递增区间是( ,+∞).
,+∞).极小值是f(
 )=0.(6分)
)=0.(6分)(2)由g(x)=x2+alnx+
 ,得g′(x)=2x+
,得g′(x)=2x+ -
- (8分)
(8分)又函数g(x)=x2+alnx+
 为[1,4]上的单调减函数.
为[1,4]上的单调减函数.则g'(x)≤0在[1,4]上恒成立,
所以不等式2x+
 -
- ≤0在[1,4]上恒成立,
≤0在[1,4]上恒成立,即a≤
 -2x2在[1,4]上恒成立. (10分)
-2x2在[1,4]上恒成立. (10分)设φ(x)=
 -2x2,显然?(x)在[1,4]上为减函数,
-2x2,显然?(x)在[1,4]上为减函数,所以?(x)的最小值为?(4)=-
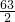 .
.∴a的取值范围是a≤-
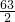 .(12分)
.(12分)分析:(1)a=-2e时,f′(x)=2x-
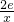 =
= ,利用x变化时,f'(x),f(x)的变化情况可求函数f(x)的单调区间和极值;
,利用x变化时,f'(x),f(x)的变化情况可求函数f(x)的单调区间和极值;(2)由g(x)=x2+alnx+
 ,得g′(x)=2x+
,得g′(x)=2x+ -
- ,由g'(x)≤0在[1,4]上恒成立,可得a≤
,由g'(x)≤0在[1,4]上恒成立,可得a≤ -2x2在[1,4]上恒成立.构造函数φ(x)=
-2x2在[1,4]上恒成立.构造函数φ(x)= -2x2,求其最小值即可.
-2x2,求其最小值即可.点评:本题考查利用倒数研究函数的单调性,着重考查函数在某点取得极值的条件,考查闭区间上的恒成立问题,突出转化思想与构造函数的思想的运用,属于难题.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|