题目内容
给出集合A={-2,-1, ,
, ,
, ,1,2,3}.已知a∈A,使得幂函数f(x)=xa为奇函数;指数函数g(x)=ax在区间(0,+∞)上为增函数.
,1,2,3}.已知a∈A,使得幂函数f(x)=xa为奇函数;指数函数g(x)=ax在区间(0,+∞)上为增函数.
(1)试写出所有符合条件的a,说明理由;
(2)判断f(x)在(0,+∞)的单调性,并证明;
(3)解方程:f[g(x)]=g[f(x)].
解:(1)a=3.…1分
∵指数函数g(x)=ax在区间(0,+∞)上为增函数,
∴a>1,
∴a只可能为2或3.
而当a=2时,幂函数f(x)=x2为偶函数,
只有当a=3时,幂函数f(x)=x3为奇函数.
(只需简单说明理由即可,无需与答案相同)…2分
(2)f(x)=x3在(0,+∞)上为增函数.…1分
证明:在(0,+∞)上任取x1,x2,x1<x2,
f(x1)-f(x2)=x13-x23
=(x1-x2)(x12+x1x2+x22)
=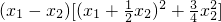 ,
,
∵x1<x2,
∴x1-x2<0,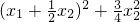 >0,
>0,
∴f(x1)-f(x2)<0,
∴f(x1)<f(x2).
∴f(x)=x3在(0,+∞)上为增函数.…3分
(3)f[g(x)]=(3x)3=33x,
g[f(x)]=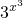 ,
,
∴33x=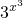 ,…2分
,…2分
根据指数函数的性质,
得3x=x3,
∴x1=0,x2= ,x3=
,x3= . …1分.
. …1分.
分析:(1)由指数函数g(x)=ax在区间(0,+∞)上为增函数,知a>1,由幂函数f(x)=xa为奇函数,知a=3.
(2)f(x)=x3在(0,+∞)上为增函数.用定义法进行证明:在(0,+∞)上任取x1,x2,x1<x2,f(x1)-f(x2)=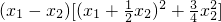 ,由x1<x2,知x1-x2<0,
,由x1<x2,知x1-x2<0,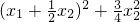 >0,f(x1)>f(x2).由此知f(x)=x3在(0,+∞)上为增函数.
>0,f(x1)>f(x2).由此知f(x)=x3在(0,+∞)上为增函数.
(3)f[g(x)]=(3x)3=33x,g[f(x)]=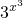 ,所以原方程等价于33x=
,所以原方程等价于33x=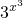 ,由此能求出结果.
,由此能求出结果.
点评:本题考查幂函数的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.
∵指数函数g(x)=ax在区间(0,+∞)上为增函数,
∴a>1,
∴a只可能为2或3.
而当a=2时,幂函数f(x)=x2为偶函数,
只有当a=3时,幂函数f(x)=x3为奇函数.
(只需简单说明理由即可,无需与答案相同)…2分
(2)f(x)=x3在(0,+∞)上为增函数.…1分
证明:在(0,+∞)上任取x1,x2,x1<x2,
f(x1)-f(x2)=x13-x23
=(x1-x2)(x12+x1x2+x22)
=
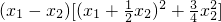 ,
,∵x1<x2,
∴x1-x2<0,
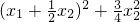 >0,
>0,∴f(x1)-f(x2)<0,
∴f(x1)<f(x2).
∴f(x)=x3在(0,+∞)上为增函数.…3分
(3)f[g(x)]=(3x)3=33x,
g[f(x)]=
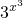 ,
,∴33x=
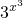 ,…2分
,…2分根据指数函数的性质,
得3x=x3,
∴x1=0,x2=
 ,x3=
,x3= . …1分.
. …1分.分析:(1)由指数函数g(x)=ax在区间(0,+∞)上为增函数,知a>1,由幂函数f(x)=xa为奇函数,知a=3.
(2)f(x)=x3在(0,+∞)上为增函数.用定义法进行证明:在(0,+∞)上任取x1,x2,x1<x2,f(x1)-f(x2)=
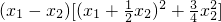 ,由x1<x2,知x1-x2<0,
,由x1<x2,知x1-x2<0,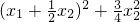 >0,f(x1)>f(x2).由此知f(x)=x3在(0,+∞)上为增函数.
>0,f(x1)>f(x2).由此知f(x)=x3在(0,+∞)上为增函数.(3)f[g(x)]=(3x)3=33x,g[f(x)]=
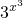 ,所以原方程等价于33x=
,所以原方程等价于33x=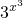 ,由此能求出结果.
,由此能求出结果.点评:本题考查幂函数的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
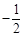 ,
,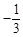 ,
,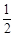 ,1,2,3}。已知a∈A,使得幂函数
,1,2,3}。已知a∈A,使得幂函数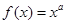 为奇函数,指数函数
为奇函数,指数函数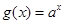 在区间(0,+∞)上为增函数。
在区间(0,+∞)上为增函数。