Question

【题目】已知函数f（x）＝2|x+2|+|x﹣3|．

（1）求不等式f（x）≥8的解集；

（2）若a＞0，b＞0，且函数F（x）＝f（x）﹣3a﹣2b有唯一零点x0，证明：f（x0）．

Answer 1

【答案】（1）（﹣∞，﹣3]∪[1，+∞）；（2）见解析

【解析】

（1）分x≤，<x<3及x≥3三种情况讨论，分别解不等式再取并集即可；

（2）易知x0=且f(x0)=5=3a+2b，即证成立，利用基本不等式即可得证．

（1）当x≤时，有(x+2)x+3≥8，即x≤3，故x≤3；

当2<x<3时，有2(x+2)x+3≥8，即x≥1，故1≤x<3；

当x≥3时，有2(x+2)+x3≥8，即，故x≥3；

综上，不等式的解集为；

（2）证明：由题意知，y=f(x)与y=3a+2b的图象有且只有一个交点，

可得x0=2且f(x0)=5=3a+2b，

即证明成立，

∵，

∴

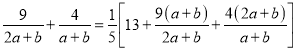
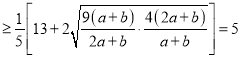，当且仅当时取等号，

∴．