题目内容
动点M的坐标(x,y)在其运动过程中总满足关系式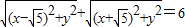 .
.(1)点M的轨迹是什么曲线?请写出它的标准方程;
(2)已知定点T(t,0)(0<t<3),若|MT|的最小值为1,求t的值.
【答案】分析:(1)由于点(x,y) 满足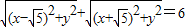 ,由椭圆的定义可知:此点的轨迹为焦点在x轴上的椭圆,且 a=3,c=
,由椭圆的定义可知:此点的轨迹为焦点在x轴上的椭圆,且 a=3,c=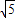 ,故b=2,由此求得椭圆的标准方程.
,故b=2,由此求得椭圆的标准方程.
(2)由于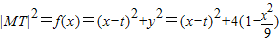 ,0≤x≤3,分
,0≤x≤3,分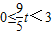 和
和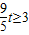 2种情况,利用|MT|的最小值为1,求出t的值.
2种情况,利用|MT|的最小值为1,求出t的值.
解答:解:(1)由于点(x,y) 满足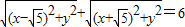 ,即点(x,y) 到两个定点(-
,即点(x,y) 到两个定点(-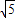 ,0)、(
,0)、(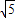 ,0)的距离之和等于常数6,
,0)的距离之和等于常数6,
由椭圆的定义可知:此点的轨迹为焦点在x轴上的椭圆,且 a=3,c=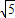 ,故b=2,故椭圆的标准方程为
,故b=2,故椭圆的标准方程为 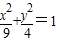 .
.
(2)由于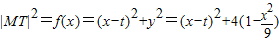 ,0≤x≤3,
,0≤x≤3,
记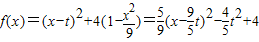 ,0≤x≤3.
,0≤x≤3.
①当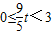 ,即
,即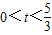 时,
时,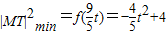 ,又
,又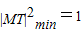 ,
,
∴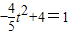 ,解得
,解得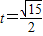 ,而
,而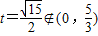 ,故舍去.
,故舍去.
②当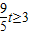 ,即
,即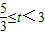 时,
时,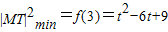 ,又
,又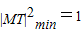 ,
,
∴t2-6t+9=1,解得t=2或t=4,而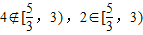 ,故t=4不符合题意,t=2符合题意.
,故t=4不符合题意,t=2符合题意.
综上可知,t=2.
点评:本题主要考查椭圆的定义、标准方程,两点间的距离公式的应用,二次函数的性质,属于基础题.
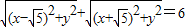 ,由椭圆的定义可知:此点的轨迹为焦点在x轴上的椭圆,且 a=3,c=
,由椭圆的定义可知:此点的轨迹为焦点在x轴上的椭圆,且 a=3,c=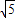 ,故b=2,由此求得椭圆的标准方程.
,故b=2,由此求得椭圆的标准方程.(2)由于
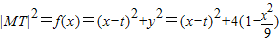 ,0≤x≤3,分
,0≤x≤3,分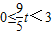 和
和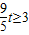 2种情况,利用|MT|的最小值为1,求出t的值.
2种情况,利用|MT|的最小值为1,求出t的值.解答:解:(1)由于点(x,y) 满足
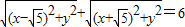 ,即点(x,y) 到两个定点(-
,即点(x,y) 到两个定点(-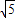 ,0)、(
,0)、(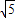 ,0)的距离之和等于常数6,
,0)的距离之和等于常数6,由椭圆的定义可知:此点的轨迹为焦点在x轴上的椭圆,且 a=3,c=
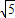 ,故b=2,故椭圆的标准方程为
,故b=2,故椭圆的标准方程为 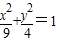 .
.(2)由于
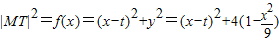 ,0≤x≤3,
,0≤x≤3,记
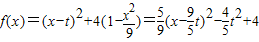 ,0≤x≤3.
,0≤x≤3.①当
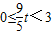 ,即
,即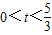 时,
时,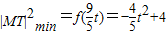 ,又
,又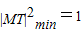 ,
,∴
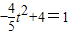 ,解得
,解得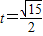 ,而
,而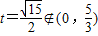 ,故舍去.
,故舍去.②当
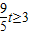 ,即
,即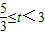 时,
时,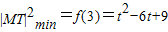 ,又
,又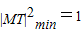 ,
,∴t2-6t+9=1,解得t=2或t=4,而
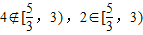 ,故t=4不符合题意,t=2符合题意.
,故t=4不符合题意,t=2符合题意.综上可知,t=2.
点评:本题主要考查椭圆的定义、标准方程,两点间的距离公式的应用,二次函数的性质,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
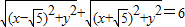 .
.