题目内容
动点M的坐标(x,y)在其运动过程中总满足关系式
+
=4.
(1)点M的轨迹是什么曲线?请写出它的标准方程;
(2)已知直线y=x+t与M的轨迹交于A、B两点,且OA⊥OB(O为原点),求t的值.
(x-
|
(x+
|
(1)点M的轨迹是什么曲线?请写出它的标准方程;
(2)已知直线y=x+t与M的轨迹交于A、B两点,且OA⊥OB(O为原点),求t的值.
分析:(1)根据
+
=4,可得(x,y)与(-
,0),(
,0)的距离之和等于常数4,由椭圆的定义可知点M的轨迹,从而可得椭圆的方程;
(2)直线y=x+t与M的轨迹方程联立,消去y,利用韦达定理及OA⊥OB,即可求得t的值.
(x-
|
(x+
|
| 3 |
| 3 |
(2)直线y=x+t与M的轨迹方程联立,消去y,利用韦达定理及OA⊥OB,即可求得t的值.
解答:0解:(1)∵
+
=4
∴(x,y)与(-
,0),(
,0)的距离之和等于常数4,
由椭圆的定义可知:此点的轨迹为焦点在x轴上的椭圆,且a=2,c=
0
∴b=1,故椭圆的方程为:
+y2=1;
(2)直线y=x+t与M的轨迹方程联立,消去y可得5x2+8tx+4t2-4=0
设A(x1,y1),B(x2,y2),则x1+x2=-
,x1x2=
,
∴y1y2=(x1+t)(x2+t)=
-
+t2=-
+
t20000000000000000000000000
∵OA⊥OB
∴x1x2+y1y2=
-
+
t2=0
∴t=±
(x-
|
(x+
|
∴(x,y)与(-
| 3 |
| 3 |
由椭圆的定义可知:此点的轨迹为焦点在x轴上的椭圆,且a=2,c=
| 3 |
∴b=1,故椭圆的方程为:
| x2 |
| 4 |
(2)直线y=x+t与M的轨迹方程联立,消去y可得5x2+8tx+4t2-4=0
设A(x1,y1),B(x2,y2),则x1+x2=-
| 8t |
| 5 |
| 4t2-4 |
| 5 |
∴y1y2=(x1+t)(x2+t)=
| 4t2-4 |
| 5 |
| 8t2 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
∵OA⊥OB
∴x1x2+y1y2=
| 4t2-4 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
∴t=±
2
| ||
| 5 |
点评:本题考查轨迹方程,考查直线与椭圆的位置关系,求得椭圆的方程,正确运用韦达定理是关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
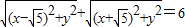 .
.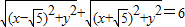 .
.