题目内容
(此题平行班做)(本小题满分12分)
某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:


(Ⅰ)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是 ,请完成上面的
,请完成上面的 列联表;
列联表;
(Ⅱ)在(1)的条件下,试运用独立性检验的思想方法分析:在犯错误概率不超过0.1%的情况下判断学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:


(Ⅰ)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是
 ,请完成上面的
,请完成上面的 列联表;
列联表; |  |  |  |
 |  |  |  |
解:(Ⅰ)如果随机抽查这个班的一名学生,抽到积极参加班级工作的学生的概率是
 ,所以积极参加班级工作的学生有
,所以积极参加班级工作的学生有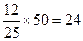 人,以此可以算出学习积极性一般且积极参加班级工作的人数为6,不太主动参加班级共工作的人数为26,学习积极性高但不太主动参加班级工作得人数为7,学习积极性高的人数为25,学习积极性一边拿的人数为25,得到变革如下:
人,以此可以算出学习积极性一般且积极参加班级工作的人数为6,不太主动参加班级共工作的人数为26,学习积极性高但不太主动参加班级工作得人数为7,学习积极性高的人数为25,学习积极性一边拿的人数为25,得到变革如下:| | 积极参加班级工作 | 不太主动参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(Ⅱ)
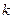 ==≈11.5,
==≈11.5,∵
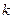 >10.828,∴有99.9%的把握认为学习积极性与对待班级工作的态度有关系.………12分
>10.828,∴有99.9%的把握认为学习积极性与对待班级工作的态度有关系.………12分略

练习册系列答案
相关题目
 .现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.
.现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.


 ( )
( )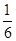
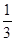
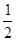
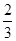


 ,求
,求 )
) 、乙两名跳高运动员一次试跳
、乙两名跳高运动员一次试跳 米高度成功的概率分别是
米高度成功的概率分别是 ,
, ,且每次试跳成功与否相互之间没有影响,求:
,且每次试跳成功与否相互之间没有影响,求: ;
; 次、
次、 次,每个基本事件为(m,n).求“
次,每个基本事件为(m,n).求“ ”的概率.
”的概率. 法考察特定化学元素的最优加人量.若进行若干次试验后存优范围[1000,m]上的一个好点为比1618,m=___________.
法考察特定化学元素的最优加人量.若进行若干次试验后存优范围[1000,m]上的一个好点为比1618,m=___________.