Question

1．已知椭圆的中心在原点，离心率为$\frac{\sqrt{2}}{2}$，F为左焦点，A为右顶点．B为短轴一顶点．
（1）求cos∠ABF；
（2）若△ABF的面积为1+$\sqrt{2}$，求椭圆的标准方程．

Answer 1

分析 （1）由$\frac{c}{a}=\frac{\sqrt{2}}{2}$，可得$a=\sqrt{2}c$=$\sqrt{2}$b，在△ABF中，|BF|=a=$\sqrt{2}$c，|AB|=$\sqrt{3}$c，|AC|=a+c=$（\sqrt{2}+1）$c．利用余弦定理可得即可得出cos∠ABF．
（2）由△ABF的面积为1+$\sqrt{2}$，可得$\frac{1}{2}|AF||OB|$=1+$\sqrt{2}$，代入解出即可得出．

解答 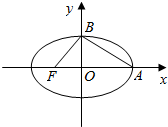解：（1）∵$\frac{c}{a}=\frac{\sqrt{2}}{2}$，可得$a=\sqrt{2}c$=$\sqrt{2}$b，
在△ABF中，|BF|=a=$\sqrt{2}$c，|AB|=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{3}$c，|AC|=a+c=$（\sqrt{2}+1）$c．
由余弦定理可得：cos∠ABF=$\frac{（\sqrt{2}c）^{2}+（\sqrt{3}c）^{2}-（\sqrt{2}+1）^{2}{c}^{2}}{2×\sqrt{2}c×\sqrt{3}c}$=$\frac{\sqrt{6}-2\sqrt{3}}{6}$．
（2）∵△ABF的面积为1+$\sqrt{2}$，
∴$\frac{1}{2}|AF||OB|$=1+$\sqrt{2}$，
∴$\frac{1}{2}（\sqrt{2}+1）c•c$=1+$\sqrt{2}$，
解得c=$\sqrt{2}$，
∴a=2，b=$\sqrt{2}$．
∴椭圆的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$．

点评 本题考查了椭圆的标准方程及其性质、余弦定理、三角形的面积计算公式，考查了推理能力与计算能力，属于中档题．