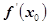题目内容
已知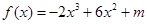 (
(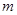 为常数)在
为常数)在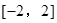 上有最小值
上有最小值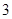 ,那么此函数在
,那么此函数在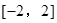 上的最大值为( )
上的最大值为( )
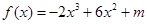 (
(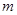 为常数)在
为常数)在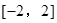 上有最小值
上有最小值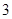 ,那么此函数在
,那么此函数在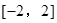 上的最大值为( )
上的最大值为( )A.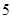 | B.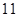 | C.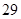 | D. |
D
试题分析:由已知,f′(x)=-6x2+12x,由-6x2+12x≥0得0≤x≤2,
因此当x∈[2,+∞),(-∞,0]时f(x)为减函数,在x∈[0,2]时f(x)为增函数,
又因为x∈[-2,2],所以得
当x∈[-2,0]时f(x)为减函数,在x∈[0,2]时f(x)为增函数,
所以f(x)min=f(0)=m=3,故有f(x)=-2x3+6x2+3
所以f(-2)=43,f(2)=11,,函数f(x)的最小值为f(-2)=43.故选D。
点评:小综合题,在某区间,导函数值非负,则函数为增函数;导函数值非正,则函数为减函数。确定最值,可遵循“求导数,求驻点,计算驻点及区间端点函数值,比较确定最值”。

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
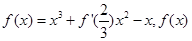 的图像在点
的图像在点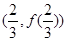 处的切线斜率是 ;
处的切线斜率是 ;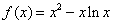 图象上的点
图象上的点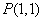 处的切线方程;
处的切线方程;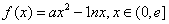 ,其中
,其中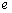 是自然对数的底数,
是自然对数的底数,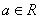
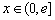 ,
,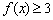 恒成立,求实数
恒成立,求实数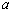 的取值范围。
的取值范围。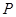 在曲线
在曲线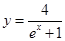 上,
上,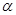 为曲线在点
为曲线在点



 等于
等于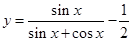 在点M(
在点M(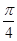 ,0)处的切线的斜率为________________.
,0)处的切线的斜率为________________.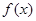 与
与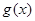 是定义在R上的两个可导函数,若
是定义在R上的两个可导函数,若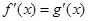 ,则
,则
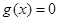
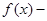
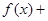
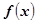 在
在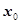 处可导,
处可导,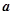 为常数,则
为常数,则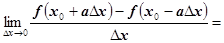 ( )
( )