题目内容
8.在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线L:ρcosθ-$\sqrt{3}$ρsinθ+1=0,曲线C的参数方程为$\left\{\begin{array}{l}x=5+cosα\\ y=sinα\end{array}\right.$(α为参数).(Ⅰ)求直线L和曲线C的普通方程;
(Ⅱ)在曲线C上求一点Q,使得Q到直线L的距离最小,并求出这个最小值.
分析 (Ⅰ)由ρ2=x2+y2,ρcosθ=x,ρsinθ=y,能求出直线L的普通方程,由cos2α+sin2α=1,能求出曲线C的普通方程.
(Ⅱ)设Q(5+cosα,sinα),求出Q到直线L的距离,由此利用三角函数性质能求出结果.
解答 解:(Ⅰ)∵直线L:ρcosθ-$\sqrt{3}$ρsinθ+1=0,
∴直线L的普通方程为:$x-\sqrt{3}y+1=0$,
∵曲线C的参数方程为$\left\{\begin{array}{l}x=5+cosα\\ y=sinα\end{array}\right.$(α为参数),
∴曲线C的普通方程为(x-5)2+y2=1.…(5分)
(Ⅱ)设Q(5+cosα,sinα),Q到直线L的距离:
$d=\frac{{|5+cosα-\sqrt{3}sinα+1|}}{2}=3-(\frac{{\sqrt{3}}}{2}sinα-\frac{1}{2}cosα)=3-sin(α-\frac{π}{6})$,
当$sin(α-\frac{π}{6})=1$时,即$α=\frac{2π}{3}$,dmin=2
此时点Q坐标为$Q(\frac{9}{2},\frac{{\sqrt{3}}}{2})$…(10分)
点评 本题考查极坐标方程、参数方程、普通方程的互化,考查点到直线距离的最小值的求法,是基础题,解题时要注意公式ρ2=x2+y2,ρcosθ=x,ρsinθ=y,cos2α+sin2α=1的合理运用.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
20.已知圆O:x2+y2=1,点M(x0,y0)是直线上x-y+2=0一点,若圆O上存在一点N,使得∠NMO=$\frac{π}{6}$,则x0的取值范围是( )
| A. | [-2,0] | B. | (0,3) | C. | [2,4] | D. | (-1,3) |
18.集合P={3,log2a},Q={a,b}且P∪Q={0,1,3},则P∩Q等于( )
| A. | {0} | B. | {3} | C. | {0}或{3} | D. | {0,3} |
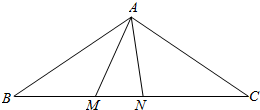 如图,在等腰△ABC中,∠BAC=120°,AB=$\sqrt{3}$,点M在线段BC上.
如图,在等腰△ABC中,∠BAC=120°,AB=$\sqrt{3}$,点M在线段BC上.