题目内容
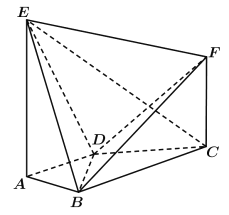
【题目】如图，
是以BC为底边的等腰三角形，DA，EB都垂直于平面ABC，且线段DA的长度大于线段EB的长度，M是BC的中点，N是ED的中点.
求证：（1）
平面EBC；
（2）
平面DAC.
【答案】（1）证明见解析（2）证明见解析
【解析】
(1)由等腰三角形的性质推出
，线面垂直的性质推出
，从而证明
平面EBC；(2)证法一：连结BN并延长，交AD的延长线于I，连结IC，证明
；证法二：在平面ABED中，分别过E，N作
，分别交AD于P，Q，取AC的中点O，连结MO，OQ，证明
；证法三：取AB的中点H，连结MH、NH，证明平面
平面DAC，根据面面平行的性质证明线面平行.
（1）因为
是以BC为底边的等腰三角形，M是BC的中点，
所以.
因为
平面ABC，
平面ABC，
所以.
又
平面EBC，
，
所以平面EBC.
（2）证法一：如图，
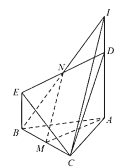
连结BN并延长，交AD的延长线于I，连结IC.
因为平面ABC，
平面ABC，
所以
，
所以
，
又N为ED的中点，所以
，
即N为BI的中点.
又M是BC的中点，
所以在
中，.
又
平面DAC，
平面DAC，
所以
平面DAC.
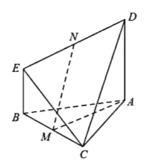
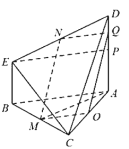
证法二：如图，
因为平面ABC，平面ABC，
所以，
所以A，B，E，D四点共面.
在平面ABED中，分别过E，N作，分别交AD于P，Q，
取AC的中点O，连结MO，OQ，
因为
，
所以四边形ABEP为平行四边形，
所以
，
因为，所以
，
又N是ED的中点，所以
，
所以
，
因为M，O分别为BC，CA的中点，
所以在中，
所以
，
所以四边形MOQN为平行四边形，
所以.
又
平面
平面DAC，
所以平面DAC.
法三：如图，
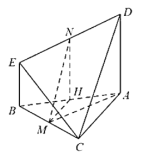
取AB的中点H，连结MH、NH.
在中，因为M，H分别为BC，BA的中点，
所以
.
又
平面DAC，
平面DAC，
所以
平面DAC.
因为平面ABC，平面ABC，
所以，又
，
所以四边形ADEB为梯形.
又N，H分别为ED，BA的中点，
所以
.
又
平面DAC，
平面DAC，
所以
平面DAC.
因为
平面NHM，
，
所以平面平面DAC，
又
平面NHM，
所以平面DAC.
