题目内容
已知O是锐角三角形△ABC的外接圆的圆心,且∠A=θ,若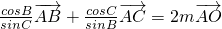 ,则m=
,则m=
- A.sinθ
- B.cosθ
- C.tanθ
- D.不能确定
A
分析:设外接圆半径为R,把已知条件化为: =
= ,左右分别与
,左右分别与 作数量积,化简可得 sin(B+C)=m,再利用诱导公式可得m=sinA=sinθ,从而得出结论.
作数量积,化简可得 sin(B+C)=m,再利用诱导公式可得m=sinA=sinθ,从而得出结论.
解答:设外接圆半径为R,则: =
= 可化为:
可化为:
 =
= (*).
(*).
易知 与
与 的夹角为2∠C,
的夹角为2∠C, 与
与 的夹角为2∠B,
的夹角为2∠B, 与
与 的夹角为0,
的夹角为0,
| |=|
|=| |=|
|=| |=R.
|=R.
则对(*)式左右分别与 作数量积,可得:
作数量积,可得:
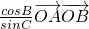 -
- +
+ -
- =-2m
=-2m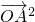 .
.
即 R2 (cos2C-1)+
R2 (cos2C-1)+ •R2(cos2B-1)=-2mR2.
•R2(cos2B-1)=-2mR2.
∴-2sinCcosB+(-2sinBcosC)=-2m,∴sinCcosB+sinBcosC=m,即 sin(B+C)=m.
因为sinA=sin[π-(B+C)]=sin(B+C)且∠A=θ,
所以,m=sinA=sinθ,
故选A.
点评:本题主要考查两个向量的数量积的运算,两角和差的正弦公式,二倍角公式的应用,属于中档题.
分析:设外接圆半径为R,把已知条件化为:
 =
= ,左右分别与
,左右分别与 作数量积,化简可得 sin(B+C)=m,再利用诱导公式可得m=sinA=sinθ,从而得出结论.
作数量积,化简可得 sin(B+C)=m,再利用诱导公式可得m=sinA=sinθ,从而得出结论.解答:设外接圆半径为R,则:
 =
= 可化为:
可化为: =
= (*).
(*).易知
 与
与 的夹角为2∠C,
的夹角为2∠C, 与
与 的夹角为2∠B,
的夹角为2∠B, 与
与 的夹角为0,
的夹角为0,|
 |=|
|=| |=|
|=| |=R.
|=R.则对(*)式左右分别与
 作数量积,可得:
作数量积,可得: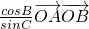 -
- +
+ -
- =-2m
=-2m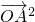 .
.即
 R2 (cos2C-1)+
R2 (cos2C-1)+ •R2(cos2B-1)=-2mR2.
•R2(cos2B-1)=-2mR2.∴-2sinCcosB+(-2sinBcosC)=-2m,∴sinCcosB+sinBcosC=m,即 sin(B+C)=m.
因为sinA=sin[π-(B+C)]=sin(B+C)且∠A=θ,
所以,m=sinA=sinθ,
故选A.
点评:本题主要考查两个向量的数量积的运算,两角和差的正弦公式,二倍角公式的应用,属于中档题.

练习册系列答案
相关题目