题目内容
(满分12分)
已知正项数列
 的前
的前 项和
项和 满足:
满足: ;设
;设 ,求数列
,求数列 的前
的前 项和的最大值。
项和的最大值。
【答案】
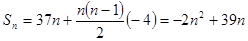
当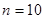 时
时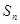 最大,最大值为
最大,最大值为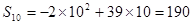
【解析】
解:当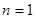 时,
时,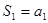 ,所以
,所以 ,即
,即 ,∴
,∴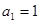 ;……1分
;……1分
当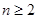 时,由
时,由 ,得
,得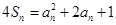 ……①, www..com
……①, www..com
∴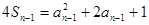 ……②
两式相减,得
……②
两式相减,得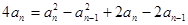
整理,得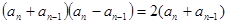 ,…………6分
,…………6分
∵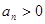 ,∴
,∴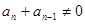 , ∴
, ∴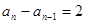 ,
,
∴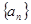 是以1为首项,以2为公差的等差数列,
是以1为首项,以2为公差的等差数列, …………8分
…………8分
∴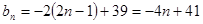 ,∴
,∴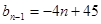 ,
,
∴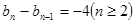 ,又
,又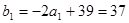
∴ 是等差数列,且
是等差数列,且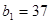 ,公差
,公差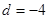 ,
,
∴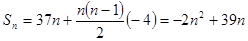 ,…………10分
,…………10分
∴当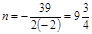 时,
时,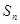 取最大值,但
取最大值,但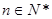 , …………11分
, …………11分
∴当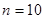 时
时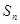 最大,最大值为
最大,最大值为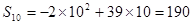 。…………12分
。…………12分

练习册系列答案
相关题目
 bc.
bc. (常数
(常数 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值. 的取值范围.
的取值范围. ,
,
 时,
时, 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围; 的图象
的图象 与函数
与函数 的图象
的图象 交于
交于 ,
, 两点,过线段
两点,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 ,
, ,问是否存在点
,问是否存在点