题目内容
(12分)已知数列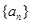 的前
的前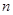 项和为
项和为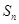 ,且
,且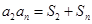 对一切正整数
对一切正整数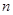 都成立.
都成立.
(1)求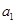 ,
,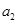 的值;
的值;
(2)设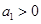 ,数列
,数列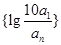 的前
的前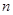 项和为
项和为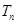 ,当
,当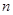 为何值时,
为何值时,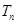 最大?并求出
最大?并求出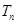 的最大值.
的最大值.
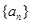 的前
的前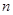 项和为
项和为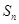 ,且
,且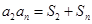 对一切正整数
对一切正整数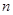 都成立.
都成立.(1)求
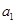 ,
,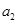 的值;
的值;(2)设
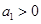 ,数列
,数列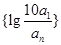 的前
的前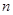 项和为
项和为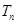 ,当
,当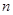 为何值时,
为何值时,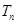 最大?并求出
最大?并求出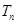 的最大值.
的最大值. (1)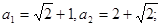
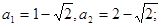
(2),n=7时,Tn取得最大值,且Tn的最大值为 T7=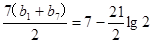
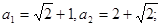
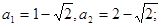
(2),n=7时,Tn取得最大值,且Tn的最大值为 T7=
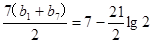
(1)令n=1则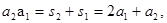
再令n=2可得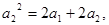 然后两方程联立可解得
然后两方程联立可解得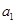 ,
,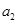 的值.
的值.
(2)在(1)的基础上,可知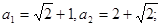
再根据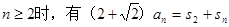 , (2+
, (2+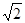 )an-1=S2+Sn-1
)an-1=S2+Sn-1
所以an=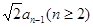 ,
,
据此可知{an}是等比数列,因而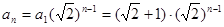 ,
,
所以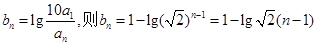 ,所以可知数列{bn}是以
,所以可知数列{bn}是以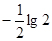 为公差,且单调递减的等差数列.然后根据bn>0可解出n的范围,从而确定Tn的最大值.
为公差,且单调递减的等差数列.然后根据bn>0可解出n的范围,从而确定Tn的最大值.
取n=1,得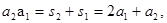 ①
①
取n=2,得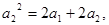 ②
②
又②-①,得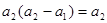 ③
③
(1)若a2="0," 由①知a1=0,
(2)若a2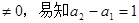 , ④
, ④
由①④得: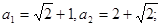
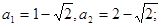
(2)当a1>0时,由(I)知,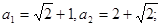
当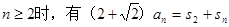 , (2+
, (2+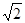 )an-1=S2+Sn-1
)an-1=S2+Sn-1
所以,an=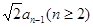
所以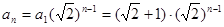
令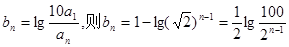
所以,数列{bn}是以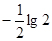 为公差,且单调递减的等差数列.
为公差,且单调递减的等差数列.
则 b1>b2>b3>>b7=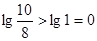
当n≥8时,bn≤b8=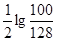
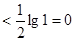
所以,n=7时,Tn取得最大值,且Tn的最大值为
T7=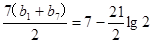
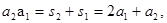
再令n=2可得
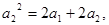 然后两方程联立可解得
然后两方程联立可解得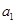 ,
,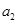 的值.
的值.(2)在(1)的基础上,可知
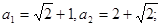
再根据
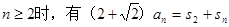 , (2+
, (2+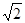 )an-1=S2+Sn-1
)an-1=S2+Sn-1 所以an=
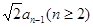 ,
,据此可知{an}是等比数列,因而
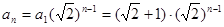 ,
,所以
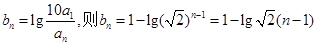 ,所以可知数列{bn}是以
,所以可知数列{bn}是以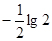 为公差,且单调递减的等差数列.然后根据bn>0可解出n的范围,从而确定Tn的最大值.
为公差,且单调递减的等差数列.然后根据bn>0可解出n的范围,从而确定Tn的最大值.取n=1,得
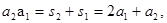 ①
① 取n=2,得
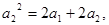 ②
② 又②-①,得
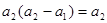 ③
③ (1)若a2="0," 由①知a1=0,
(2)若a2
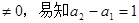 , ④
, ④ 由①④得:
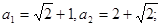
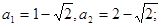
(2)当a1>0时,由(I)知,
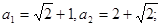
当
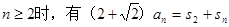 , (2+
, (2+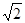 )an-1=S2+Sn-1
)an-1=S2+Sn-1 所以,an=
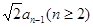
所以
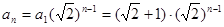
令
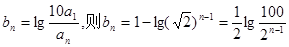
所以,数列{bn}是以
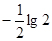 为公差,且单调递减的等差数列.
为公差,且单调递减的等差数列. 则 b1>b2>b3>>b7=
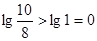
当n≥8时,bn≤b8=
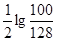
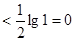
所以,n=7时,Tn取得最大值,且Tn的最大值为
T7=
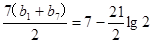

练习册系列答案
相关题目
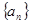 满足
满足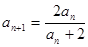 (
(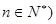 ,
,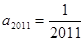 .
. ,且
,且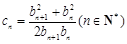 ,求证:
,求证: 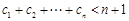 .
.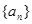 满足
满足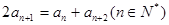 ,它的前
,它的前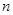 项和为
项和为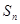 ,且
,且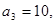
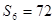 .
.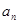 ,
, 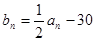 ,求数列
,求数列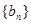 的前
的前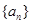 的前
的前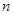 项和为
项和为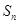 ,则
,则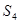 ,
,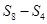 ,
,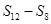 ,
,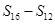 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列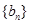 的前
的前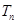 ,则
,则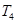 ,______,________
,______,________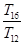 成等比数列.
成等比数列. 中,
中, ,则
,则 ( )
( )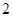
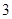
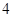
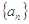 前
前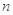 项和为
项和为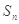 ,
,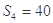 ,
,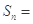 210,
210, 130,则
130,则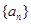 中,
中,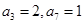 ,且数列
,且数列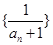 是等差数列,则
是等差数列,则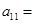 ( )
( )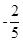
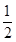
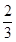
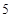
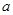 所代表的正整数是
所代表的正整数是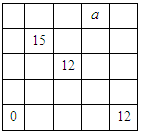
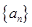 中,
中,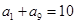 ,则
,则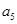 的值为( )
的值为( )