题目内容
已知直线l:y=kx+1与双曲线C:3x2-y2=1的左支交于点A,右支交于点B
(1)求k的取值范围;
(2)若直线l与y轴交于点P,且满足|PB|=2|PA|,求直线l的方程.
解:(1)由 (1)
(1)
因直线l与双曲线在左、右两支分别交于A、B两点,
所以 ,解得k2<3,所以k的取值范围为
,解得k2<3,所以k的取值范围为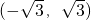
(2)因|PB|=2|PA|且点P在线段AB上,故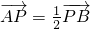 ,设A(x1,y1),B(x2,y2),由于点P的坐标为(0,1),所以有
,设A(x1,y1),B(x2,y2),由于点P的坐标为(0,1),所以有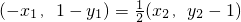 ,
,
所以 ,
,
于是可得: ,
,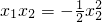
所以有: ,结合(1)有
,结合(1)有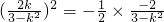 ,解得
,解得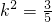 .
.
又由于点A在左支,点B在右支,并结合|PB|=2|PA|知k>0,所以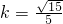 ,从而直线l的方程为
,从而直线l的方程为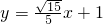 .
.
分析:(1)把直线与双曲线方程联立消去y,利用判别式大于0和两根之积小于0联立求得k的范围.
(2)因|PB|=2|PA|且点P在线段AB上,故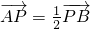 ,设A(x1,y1),B(x2,y2),利用向量关系得出A,B两点的坐标之间的关系式,结合(1)中一元二次方程根与系数的关系建立等式即可求出直线l的斜率,从而写出直线l的方程.
,设A(x1,y1),B(x2,y2),利用向量关系得出A,B两点的坐标之间的关系式,结合(1)中一元二次方程根与系数的关系建立等式即可求出直线l的斜率,从而写出直线l的方程.
点评:本题主要考查了直线与圆锥曲线的关系.考查了函数思想的应用,圆锥曲线与向量知识的综合.
 (1)
(1)因直线l与双曲线在左、右两支分别交于A、B两点,
所以
 ,解得k2<3,所以k的取值范围为
,解得k2<3,所以k的取值范围为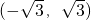
(2)因|PB|=2|PA|且点P在线段AB上,故
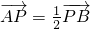 ,设A(x1,y1),B(x2,y2),由于点P的坐标为(0,1),所以有
,设A(x1,y1),B(x2,y2),由于点P的坐标为(0,1),所以有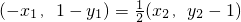 ,
,所以
 ,
,于是可得:
 ,
,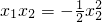
所以有:
 ,结合(1)有
,结合(1)有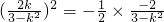 ,解得
,解得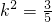 .
.又由于点A在左支,点B在右支,并结合|PB|=2|PA|知k>0,所以
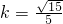 ,从而直线l的方程为
,从而直线l的方程为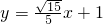 .
.分析:(1)把直线与双曲线方程联立消去y,利用判别式大于0和两根之积小于0联立求得k的范围.
(2)因|PB|=2|PA|且点P在线段AB上,故
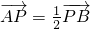 ,设A(x1,y1),B(x2,y2),利用向量关系得出A,B两点的坐标之间的关系式,结合(1)中一元二次方程根与系数的关系建立等式即可求出直线l的斜率,从而写出直线l的方程.
,设A(x1,y1),B(x2,y2),利用向量关系得出A,B两点的坐标之间的关系式,结合(1)中一元二次方程根与系数的关系建立等式即可求出直线l的斜率,从而写出直线l的方程.点评:本题主要考查了直线与圆锥曲线的关系.考查了函数思想的应用,圆锥曲线与向量知识的综合.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足
如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足