题目内容
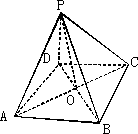
 如图,P是四边形ABCD所在平面外一点,O是AC与BD的交点,且PO⊥平面ABCD.当四边形ABCD满足下列条件
如图,P是四边形ABCD所在平面外一点,O是AC与BD的交点,且PO⊥平面ABCD.当四边形ABCD满足下列条件①②③
①②③
时,点P到四边形四条边的距离相等.①正方形;②圆的外切四边形;③菱形;④矩形.
分析:连接PA、PB、PC、PD,若要使P到四边形四条边的距离相等,则P在底面的射影O到四边形各边的距离也相等.过O点作出到边的垂线段,可以利用线面垂直的性质证明相应的直角三角形全等,从而得到三角形的斜边对应相等,用此性质不难判断出符合条件的选项为①②③
解答:解:连接PA、PB、PC、PD,作OE⊥AB于E,作OF⊥BC于F,连接PE、PF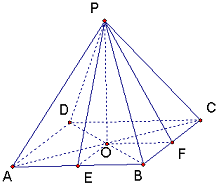
∵PO⊥平面ABCD
∴△POE、△POF均为直角三角形
若OE=OF,则根据边角边公理,可得△POE≌△POF
则有PE=PF
又∵AB⊥OE,AB⊥PO,OE∩PO=O
∴AB⊥平面POE,可得PE是P到AB的距离
同理可得PF是P到BC的距离.
因此可得:OE=OF可答出推出P到AB的距离等于P到BC的距离.
同理可以得到P到其它边的距离也是相等的,反过来也成立.
故“O到边的距离相等”等价于“P到边的距离相等”
因为正方形、菱形和圆外切四边形都是有内切圆的四边形,
内切圆的圆心到四条边的距离相等
所以满足条件的应该是正方形、菱形和圆外切四边形
故答案为:①②③

∵PO⊥平面ABCD
∴△POE、△POF均为直角三角形
若OE=OF,则根据边角边公理,可得△POE≌△POF
则有PE=PF
又∵AB⊥OE,AB⊥PO,OE∩PO=O
∴AB⊥平面POE,可得PE是P到AB的距离
同理可得PF是P到BC的距离.
因此可得:OE=OF可答出推出P到AB的距离等于P到BC的距离.
同理可以得到P到其它边的距离也是相等的,反过来也成立.
故“O到边的距离相等”等价于“P到边的距离相等”
因为正方形、菱形和圆外切四边形都是有内切圆的四边形,
内切圆的圆心到四条边的距离相等
所以满足条件的应该是正方形、菱形和圆外切四边形
故答案为:①②③
点评:本题着重考查了直线和平面的性质的应用,属于中档题.对于棱锥而言,若顶点到底面各边距离相等,则顶点在底面的射影到各边的距离相等,这是棱锥的一个常见的性质.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
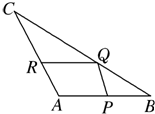 如图,△ABC是一块边长AB=3m,AC=5m,BC=7m的剩余角料.现要从中裁剪出一块面积最大的平行四边形用料APQR,要求顶点P,Q,R分别在边AB,BC,CA上.问点Q在BC边上的什么位置时,剪裁符合要求?并求这个最大值.
如图,△ABC是一块边长AB=3m,AC=5m,BC=7m的剩余角料.现要从中裁剪出一块面积最大的平行四边形用料APQR,要求顶点P,Q,R分别在边AB,BC,CA上.问点Q在BC边上的什么位置时,剪裁符合要求?并求这个最大值.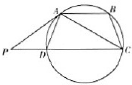 如图,ABCD是圆的内接四边形,AB∥CD,过A点的圆的切线与CD的延长线交于P点,证明:
如图,ABCD是圆的内接四边形,AB∥CD,过A点的圆的切线与CD的延长线交于P点,证明: 如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):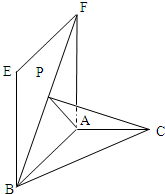 (2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=
(2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=