题目内容
解关于x的方程.(1)log(x+a)2x=2.
(2)log4(3-x)+log0.25(3+x)=log4(1-x)+log0.25(2x+1);
(3)(
3+2
|
3-2
|
(4) lg(ax-1)-lg(x-3)=1.
分析:利用等价转化思想将这些方程都转化为与之等价的代数方程,通过求解代数方程达到求解该方程的目的.注意对数中真数大于零的特点.
(1)要注意对数式与指数式的转化关系;
(2)利用对数运算性质进行转化变形;
(3)注意到两项的联系,利用整体思想先求出整体,进一步求出方程的根;
(4)利用对数的运算性质进行转化与变形是解决本题的关键.注意对字母的讨论.
(1)要注意对数式与指数式的转化关系;
(2)利用对数运算性质进行转化变形;
(3)注意到两项的联系,利用整体思想先求出整体,进一步求出方程的根;
(4)利用对数的运算性质进行转化与变形是解决本题的关键.注意对字母的讨论.
解答:解:(1)该方程可变形为2x=(x+a)2,即x=1-a±
(当a≤
时),当x=1-a-
时,x+a=1-
<0,故舍去.因此该方程的根为x=1-a+
(当a≤
时),当a>
时,原方程无根.
(2)该方程可变形为log4
=log4
,即
=
,整理得x2-7x=0,解出x=0或者x=7(不满足真数大于0,舍去).故该方程的根为x=0.
(3)该方程变形为(
)x+(
)x=6,即(
+1)x+(
-1)x=6,令t=(
+1)x,则可得出t+
=6,解得t=3±2
=(
±1)2,因此x=±2.该方程的根为±2.
(4)原方程等价于
,由
=10得出ax-1=10x-30,该方程当a=10时没有根,当a≠10时,x=
,要使得是原方程的根,需满足ax-1>0,且x-3>0.解出a∈(
,10).因此当a∈(
,10)时,原方程的根为x=
,当a∈(-∞,
]∪[10,+∝)时,原方程无根.
| 1-2a |
| 1 |
| 2 |
| 1-2a |
| 1-2a |
| 1-2a |
| 1 |
| 2 |
| 1 |
| 2 |
(2)该方程可变形为log4
| 3-x |
| 3+x |
| 1-x |
| 2x+1 |
| 3-x |
| 3+x |
| 1-x |
| 2x+1 |
(3)该方程变形为(
(
|
(
|
| 2 |
| 2 |
| 2 |
| 1 |
| t |
| 2 |
| 2 |
(4)原方程等价于
|
| ax-1 |
| x-3 |
| -29 |
| a-10 |
| 1 |
| 3 |
| 1 |
| 3 |
| -29 |
| a-10 |
| 1 |
| 3 |
点评:本题考查代数方程的求解,注意方程的等价变形,注意对数形式方程的真数大于零的特征,注意对所求的根进行检验,对含字母的方程要注意讨论.

练习册系列答案
相关题目
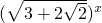 +
+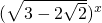 =6;
=6;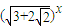 +
+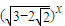 =6;
=6;