题目内容
在袋中装20个小球，其中彩球有n个红色、5个蓝色、10个黄色，其余为白球．求：
（1）如果从袋中取出3个都是相同颜色彩球（无白色）的概率是
| 13 | 114 |
（2）根据（1）的结论，计算从袋中任取3个小球至少有一个是红球的概率．
分析：（1）由题意知本题是一个等可能事件的概率问题，试验包含的所有事件是从20个球中取3个球球，3个球全为红色，3个球全为蓝色，3个球全为黄色是互斥的，根据互斥事件的概率得到结果．
（2）由题意知3个球中至少有一个是红球的对立事件是3个球中没有红球，算出没有红球的概率，用对立事件的概率公式得到结果．
（2）由题意知3个球中至少有一个是红球的对立事件是3个球中没有红球，算出没有红球的概率，用对立事件的概率公式得到结果．
解答：解：（1）由题意知本题是一个等可能事件的概率问题，
试验包含的所有事件是从20个球中取3个球球的种数为C203=1140．
设“3个球全为红色”为事件A，
“3个球全为蓝色”为事件B，
“3个球全为黄色”为事件C．
P（B）=
=
，P（C）=
=
．
∵A、B、C为互斥事件，
∴P（A+B+C）=P（A）+P（B）+P（C），
即
=P（A）+
+
P（A）=0
∴取3个球全为红球的个数≤2．
又∵n≥2，故n=2．
（2）记“3个球中至少有一个是红球”为事件D．
则
为“3个球中没有红球”．
P（D）=1-P（
）=1-
=
或
P（D）=
=
．
试验包含的所有事件是从20个球中取3个球球的种数为C203=1140．
设“3个球全为红色”为事件A，
“3个球全为蓝色”为事件B，
“3个球全为黄色”为事件C．
P（B）=
| ||
|
| 10 |
| 1140 |
| ||
|
| 120 |
| 1140 |
∵A、B、C为互斥事件，
∴P（A+B+C）=P（A）+P（B）+P（C），
即
| 13 |
| 114 |
| 10 |
| 1140 |
| 120 |
| 1140 |
P（A）=0
∴取3个球全为红球的个数≤2．
又∵n≥2，故n=2．
（2）记“3个球中至少有一个是红球”为事件D．
则
. |
| D |
P（D）=1-P（
. |
| D |
| ||
|
| 27 |
| 95 |
P（D）=
| ||||||||
|
| 27 |
| 95 |
点评：本题考查等可能事件的概率和互斥事件，分清互斥事件和对立事件之间的关系，互斥事件是不可能同时发生的事件，对立事件是指一个不发生，另一个一定发生的事件．
练习册系列答案
相关题目
，且n≥2，那么，袋中的红球共有几个？
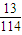，且n≥2，那么，袋中的红球共有几个？