题目内容
在袋中装20个小球,其中彩球有n个红色、5个蓝色、10个黄色,其余为白球.求:(1)如果从袋中取出3个都是相同颜色彩球(无白色)的概率是![]() ,且n≥2,那么,袋中的红球共有几个?
,且n≥2,那么,袋中的红球共有几个?
(2)根据(1)的结论,计算从袋中任取3个小球至少有一个是红球的概率.
解:(1)取3个球的种数为![]() =1 140.
=1 140.
设“3个球全为红色”为事件A,“3个球全为蓝色”为事件B,“3个球全为黄色”为事件C.
P(B)=![]() ,P(C)=
,P(C)=![]() .
.
∵A、B、C为互斥事件.
∴P(A+B+C)=P(A)+P(B)+P(C),
即![]() =P(A)+
=P(A)+![]()
![]() P(A)=0
P(A)=0![]() 取3个球全为红球的个数≤2.又∵n≥2,故n=2.
取3个球全为红球的个数≤2.又∵n≥2,故n=2.
(2)记“3个球中至少有一个是红球”为事件D,则![]() 为“3个球中没有红球”.
为“3个球中没有红球”.
P(D)=1-P(![]() )=
)=![]() 或P(D)=
或P(D)=![]() .
.

练习册系列答案
相关题目
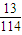 ,且n≥2,那么,袋中的红球共有几个?
,且n≥2,那么,袋中的红球共有几个?