题目内容
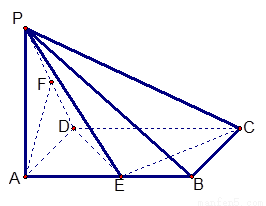
已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点.
(1)求证:BD⊥AE;
(2)求四棱锥P-ABCD的侧面积.
(1)求证:BD⊥AE;
(2)求四棱锥P-ABCD的侧面积.

分析:(1)由正视图与侧视图知PC⊥平面ABCD,由俯视图知底面为边长为1的正方形,通过证明BD⊥平面PAC,可证BD⊥AE;
(2)证明,△PAB和△PAD都为直接三角形,代人数据求出各侧面的面积,再相加.
(2)证明,△PAB和△PAD都为直接三角形,代人数据求出各侧面的面积,再相加.
解答:解:(1)由正视图与侧视图知PC⊥平面ABCD,BD?平面ABCD,∴PC⊥BD,
由俯视图知底面为边长为1的正方形,∴BD⊥AC,
又AC∩PC=C,
∴BD⊥平面PAC,AE?平面PAC,
∴BD⊥AE;
(2)∵AB⊥BC,BC为PB在底面ABCD内的摄影,
∴AB⊥PB,△PAB为直角三角形,
同理可证△PAD也为直接三角形,
∵PC=2,
∴PB=PD=
,
∴四棱锥P-ABCD的侧面积S=S△PAB+S△PBC+S△PCD+S△PAD=
×1×
+
×1×2+
×1×2+
×1×
=2+
.
由俯视图知底面为边长为1的正方形,∴BD⊥AC,
又AC∩PC=C,
∴BD⊥平面PAC,AE?平面PAC,
∴BD⊥AE;
(2)∵AB⊥BC,BC为PB在底面ABCD内的摄影,
∴AB⊥PB,△PAB为直角三角形,
同理可证△PAD也为直接三角形,
∵PC=2,
∴PB=PD=
| 5 |
∴四棱锥P-ABCD的侧面积S=S△PAB+S△PBC+S△PCD+S△PAD=
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
点评:本题考查了由三视图求几何体的体积,解题的关键是由三视图判断几何体中线面的位置关系及三视图的数据所对应的几何量.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
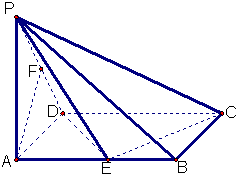 已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,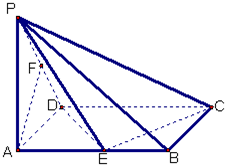 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.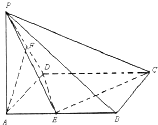 (2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点.
(2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点.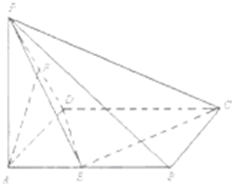 (2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=2,PA=AD=1,E,F分别是AB、PD的中点.
(2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=2,PA=AD=1,E,F分别是AB、PD的中点.