题目内容
(本小题满分14分)
已知函数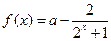 。
。
(1)求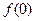 ;
;
(2)探究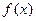 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(3)若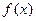 为奇函数,求满足
为奇函数,求满足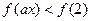 的
的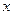 的范围。
的范围。
已知函数
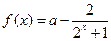 。
。 (1)求
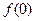 ;
;(2)探究
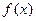 的单调性,并证明你的结论;
的单调性,并证明你的结论;(3)若
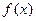 为奇函数,求满足
为奇函数,求满足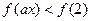 的
的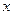 的范围。
的范围。(1)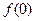 =
=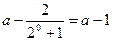
(2)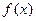 在R上单调递增,证明略。
在R上单调递增,证明略。
(3)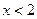
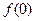 =
=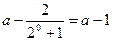
(2)
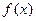 在R上单调递增,证明略。
在R上单调递增,证明略。(3)
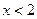
解:(1)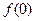 =
=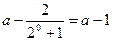 ……………………….2分
……………………….2分
(2)∵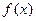 的定义域为R ∴任取
的定义域为R ∴任取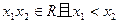
则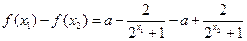 =
=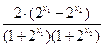 …………4分
…………4分
∵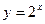 在R是单调递增且
在R是单调递增且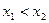
∴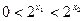 ∴
∴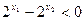
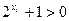
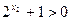
∴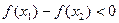 即
即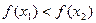 ………………………6分
………………………6分
∴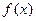 在R上单调递增 …………………………8分
在R上单调递增 …………………………8分
(3) ∵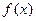 是奇函数
是奇函数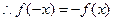 ,即
,即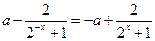 ,
,
解得: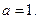 ……………………10分
……………………10分
(或用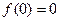 去做)
去做)
∴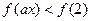 即为
即为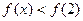 ………………………11分
………………………11分
又∵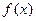 在R上单调递增
在R上单调递增
∴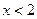 ……………14分
……………14分
(或代入化简亦可)
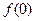 =
=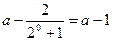 ……………………….2分
……………………….2分(2)∵
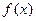 的定义域为R ∴任取
的定义域为R ∴任取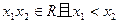
则
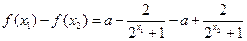 =
=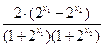 …………4分
…………4分∵
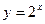 在R是单调递增且
在R是单调递增且
∴
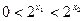 ∴
∴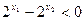
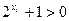
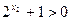
∴
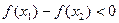 即
即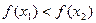 ………………………6分
………………………6分∴
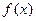 在R上单调递增 …………………………8分
在R上单调递增 …………………………8分(3) ∵
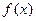 是奇函数
是奇函数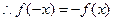 ,即
,即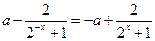 ,
,解得:
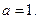 ……………………10分
……………………10分(或用
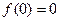 去做)
去做)∴
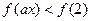 即为
即为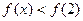 ………………………11分
………………………11分又∵
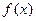 在R上单调递增
在R上单调递增∴
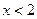 ……………14分
……………14分(或代入化简亦可)

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 ,
, ,
,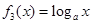 (其中
(其中 且
且 ),在同一坐标系中画出其中两个函数在x≥0且y≥0的范围内的大致图象,其中正确的是( )
),在同一坐标系中画出其中两个函数在x≥0且y≥0的范围内的大致图象,其中正确的是( )



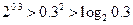 ,(2)
,(2)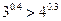 ,(3)
,(3)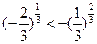 ,
, 在R上是奇函数,则
在R上是奇函数,则 的图像是 ( )
的图像是 ( )
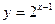 的反函
的反函 数是
数是



 =_________.
=_________. 大小的顺序是 ( )
大小的顺序是 ( )



 b
b b
b 的图象恒过定点A,且点A在直线
的图象恒过定点A,且点A在直线 上
上 ,则
,则 的最小值为( )
的最小值为( )