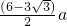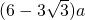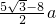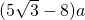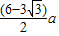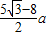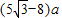题目内容
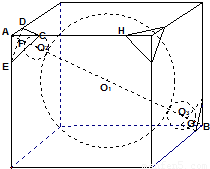
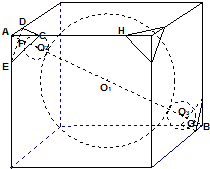 如图,一个棱长为a的立方体内有1个大球和8个小球,大球与立方体的六个面都相切,每个小球与大球外切且与共顶点的三个面也相切,现在把立方体的每个角都截去一个三棱锥,截面都为正三角形并与小球相切,变成一个新的立体图形,则原立方体的每条棱还剩余( )
如图,一个棱长为a的立方体内有1个大球和8个小球,大球与立方体的六个面都相切,每个小球与大球外切且与共顶点的三个面也相切,现在把立方体的每个角都截去一个三棱锥,截面都为正三角形并与小球相切,变成一个新的立体图形,则原立方体的每条棱还剩余( )分析:先得出大球的半径为
,设小球的半径r,利用三角形的内切圆半径公式用a 来表示r,再设小球切截面CDE于F,表示出AF的长,最后利用等积法求得结果即可.
| a |
| 2 |
解答:解:大球的半径为
,设小球的半径r,则2
r+2r+a=
a⇒r=
a=
a
设小球切截面CDE于F,则AF=
=
a,
设AC=x,利用等积法求得x=
AF=
a,所以CH=a-2AF=(5
-8)a
故选D.
| a |
| 2 |
| 3 |
| 3 |
| ||
2(
|
2-
| ||
| 2 |
设小球切截面CDE于F,则AF=
| ||
| 2 |
3
| ||
| 2 |
设AC=x,利用等积法求得x=
| 3 |
9-5
| ||
| 2 |
| 3 |
故选D.
点评:本题是基础题,考查棱柱的结构特征知识,本题的解答采用截面法,平面几何的应用,考查空间想象能力.

练习册系列答案
相关题目
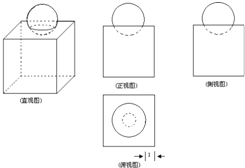 如图是一个简单的组合体的直观图与三视图.如图是一个棱长为4的正方体,正上面放一个球,且球的一部分嵌入正方体中,则球的半径是( )
如图是一个简单的组合体的直观图与三视图.如图是一个棱长为4的正方体,正上面放一个球,且球的一部分嵌入正方体中,则球的半径是( )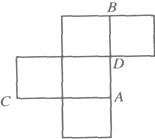 如图是一个棱长为1的无盖正方体盒子的平面展开图,A,B,C,D为其上四个点,
如图是一个棱长为1的无盖正方体盒子的平面展开图,A,B,C,D为其上四个点,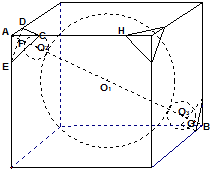 如图,一个棱长为a的立方体内有1个大球和8个小球,大球与立方体的六个面都相切,每个小球与大球外切且与共顶点的三个面也相切,现在把立方体的每个角都截去一个三棱锥,截面都为正三角形并与小球相切,变成一个新的立体图形,则原立方体的每条棱还剩余
如图,一个棱长为a的立方体内有1个大球和8个小球,大球与立方体的六个面都相切,每个小球与大球外切且与共顶点的三个面也相切,现在把立方体的每个角都截去一个三棱锥,截面都为正三角形并与小球相切,变成一个新的立体图形,则原立方体的每条棱还剩余