题目内容
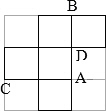
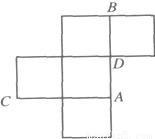
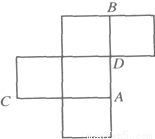
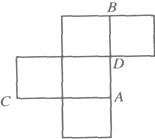 如图是一个棱长为1的无盖正方体盒子的平面展开图,A,B,C,D为其上四个点,
如图是一个棱长为1的无盖正方体盒子的平面展开图,A,B,C,D为其上四个点,(1)请画出无盖正方体盒子的示意图,并标出A,B,C,D四点;
(2)求以A,B,C,D为顶点的三棱锥的体积.
分析:(1)先将正方形还原,根据已知展开图中A,B,C,D四点的位置,结合正方体的几何特征,可标出还原后四点的位置;
(2)根据(1)中四点的位置,结合棱长为1,代入棱锥体积公式,可得答案.
(2)根据(1)中四点的位置,结合棱长为1,代入棱锥体积公式,可得答案.
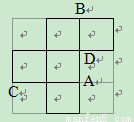
解答:解:(1)还原后,A,B,C,D四点的位置,如图所示:
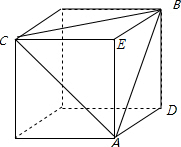
(2)由(1)可得:
以A,B,C,D为顶点的三棱锥的体积
VC-ABD=
×(
×BD×AD)×CE
=
×(
×1×1)×1
=

(2)由(1)可得:
以A,B,C,D为顶点的三棱锥的体积
VC-ABD=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 6 |
点评:本题考查的知识点是棱锥的体积,正方体的几何特征,熟练掌握正方体的几何特征,正确画出还原图中,A,B,C,D四点位置是解答的关键.

练习册系列答案
相关题目