题目内容
双曲线G的中心在原点O,并以抛物线![]() 的顶点为右焦点,以此抛物线的准线为右准线.
的顶点为右焦点,以此抛物线的准线为右准线.
(1)求双曲线G的方程;
(2)设直线l:y=kx+3与双曲线G相交于A、B两点,
①当k为何值时,原点O在以AB为直径的圆上?
②是否存在这样的实数k,使A、B两点关于直线y=mx(m为常数)对称?若存在,求出k的值;若不存在,说明理由.
答案:
解析:
解析:
|
解:(1)抛物线 准线为 设双曲线G为 ∴双曲线G的方程为 (2)①由 又由 设 ∵若原点O在AB为直径的圆上,有OA⊥OB,KOA·KOB=-1, 化简为 ②设这样的实数k存在,则有 由②③得, 即 这与km=-1矛盾,所以适合条件的k不存在.(14分) |

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
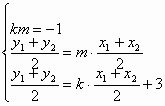
 ,使得
,使得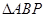 的面积最大时点P的坐标.
的面积最大时点P的坐标.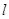 ,使得
,使得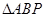 的面积最大时点P的坐标.
的面积最大时点P的坐标.