题目内容
20. 如图,已知⊙O的直径为AB,点C为⊙O上异于A,B的一点,BC⊥VA,AC⊥VB.
如图,已知⊙O的直径为AB,点C为⊙O上异于A,B的一点,BC⊥VA,AC⊥VB.(Ⅰ)求证:VC⊥平面ABC;
(Ⅱ)已知AC=1,VC=2,AB=3,点M为线段VB的中点,求两面角B-MA-C的正弦值.
分析 (Ⅰ)通过直径所对的圆周角为直径及线面垂直的判定定理可得结论;
(Ⅱ)以C为原点,以CA、CB、CV所在直线分别为x、y、z轴建立空间直角坐标系C-xyz,则所求角的余弦值为平面BMA的法向量与平面CMA的法向量的夹角的余弦值的绝对值,计算即可.
解答  (Ⅰ)证明:∵AB是⊙O的直径,∴AC⊥BC,
(Ⅰ)证明:∵AB是⊙O的直径,∴AC⊥BC,
又∵BC⊥VA,AC∩VA=A,
∴BC⊥平面VAC,∴BC⊥VC,
又∵AC⊥VB且AC⊥BC,VB∩BC=B,
∴AC⊥平面VBC,∴AC⊥VC,
又∵BC∩AC=C,∴VC⊥平面ABC;
(Ⅱ)解:∵BC⊥VC,VC⊥平面ABC,
∴VC⊥BC,VC⊥AC,
又AC⊥BC,∴以C为原点,以CA、CB、CV所在直线分别为x、y、z轴建立空间直角坐标系C-xyz如图,
则A(1,0,0),B(0,2$\sqrt{2}$,0),V(0,0,2),∴M(0,$\sqrt{2}$,1),
∴$\overrightarrow{AM}$=(-1,$\sqrt{2}$,1),$\overrightarrow{AB}$=(-1,2$\sqrt{2}$,0),$\overrightarrow{CA}$=(1,0,0),
设平面BMA的法向量为$\overrightarrow{m}$=(x,y,z),
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AB}=0}\\{\overrightarrow{m}•\overrightarrow{AM}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-x+\sqrt{2}y+z=0}\\{-x+2\sqrt{2}y=0}\end{array}\right.$,可取$\overrightarrow{m}$=(2$\sqrt{2}$,1,$\sqrt{2}$),
设平面CMA的法向量为$\overrightarrow{n}$=(x,y,z),
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CA}=0}\\{\overrightarrow{n}•\overrightarrow{AM}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-x+\sqrt{2}y+z=0}\\{-x=0}\end{array}\right.$,可取$\overrightarrow{n}$=(0,1,-$\sqrt{2}$),
∴$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-1}{\sqrt{33}}$=-$\frac{\sqrt{33}}{33}$,
∴两面角B-MA-C的正弦值为$\sqrt{1-(-\frac{\sqrt{33}}{33})^{2}}$=$\frac{4\sqrt{66}}{33}$.
点评 本题考查直线与平面垂直的判定,二面角的计算,考查空间想象能力,计算能力,注意解题方法的积累,属于中档题.

 每课必练系列答案
每课必练系列答案| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不能确定 |
| A. | f(k)+k-1 | B. | f(k)+k+1 | C. | f(k)+k | D. | f(k)+k-2 |

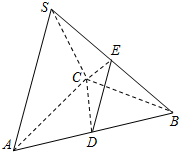 如图,在三棱锥S-ABC中,底面ABC是正三角形,AB=4,SA=SC=2$\sqrt{3}$,侧面SAC⊥底面ABC,D,E分别为AB,SB的中点.
如图,在三棱锥S-ABC中,底面ABC是正三角形,AB=4,SA=SC=2$\sqrt{3}$,侧面SAC⊥底面ABC,D,E分别为AB,SB的中点.