题目内容
已知向量 ,
, ,(
,( ,且
,且 为常数),设函数
为常数),设函数 ,若
,若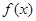 的最大值为1.
的最大值为1.
(1)求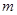 的值,并求
的值,并求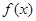 的单调递增区间;
的单调递增区间;
(2)在 中,角
中,角 、
、 、
、 的对边
的对边 、
、 、
、 ,若
,若 ,且
,且 ,试判断三角形的形状.
,试判断三角形的形状.
(1)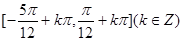 ;(2)
;(2) 是直角三角形
是直角三角形
解析试题分析:(1)先由 求出解析式,再由
求出解析式,再由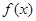 的最大值为1求出
的最大值为1求出 ,由三角函数的单调性求出单调递增区间为
,由三角函数的单调性求出单调递增区间为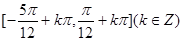 ;(2)先由
;(2)先由 解得
解得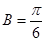 ,由正弦定理得
,由正弦定理得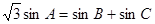 ,从而求得
,从而求得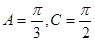 ,确定
,确定 是直角三角形.
是直角三角形.
试题解析:(1) ,
,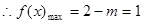 ,
, .
.
由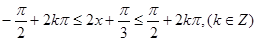 得单调递增区间为
得单调递增区间为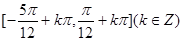 .
.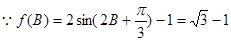 ,解得
,解得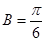 .
.
又 ,由正弦定理得:
,由正弦定理得: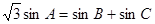 ,
,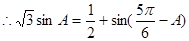 ,
,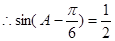 ,故:
,故: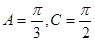 ,
,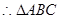 是直角三角形.
是直角三角形.
考点:1.向量数量积的坐标运算;2.三角函数的单调性;3.三角形形状的判定

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
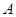 、
、 、
、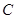 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点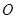 ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为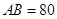
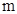 ,
,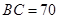
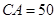
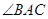 的大小;
的大小;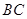 的距
的距 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
. 的值;
的值; ,且
,且 ,求
,求 和
和 的值.
的值. ,设函数
,设函数 +1
+1 ,
,  ,求
,求 的值;
的值; ,且满足
,且满足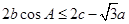 ,求
,求
 中,内角
中,内角 所对的边长分别为
所对的边长分别为 ,
, ,
, ,
, .
. 的最大值为2.
的最大值为2. 在
在 上的单调递减区间;
上的单调递减区间; 中,
中, ,角
,角 所对的边分别是
所对的边分别是 ,且
,且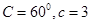 ,求
,求 是
是 的内角,
的内角, 分别是其对边长,且
分别是其对边长,且 .
. ,求
,求 的长;
的长; 的对边
的对边 ,求
,求 .
. ,求该三角形内切圆半径的取值范围。
,求该三角形内切圆半径的取值范围。 中,
中, 分别是三个内角
分别是三个内角 的对边.若
的对边.若 ,
, ,
,  的值;
的值; .
.