题目内容
函数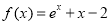 的零点所在的一个区间是
的零点所在的一个区间是
A.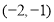 B.
B. 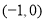 C.
C.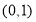 D.
D.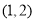
C
【解析】
试题分析:判定连续函数在区间 上存在零点的方法
上存在零点的方法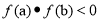 .由
.由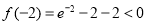 ,
,
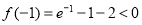 ,
,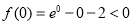 ,
, ,
, ,所以
,所以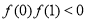 故选C
故选C
考点:函数的零点的判定定理,以及学生的计算能力.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
题目内容
函数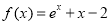 的零点所在的一个区间是
的零点所在的一个区间是
A.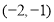 B.
B. 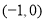 C.
C.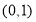 D.
D.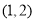
C
【解析】
试题分析:判定连续函数在区间 上存在零点的方法
上存在零点的方法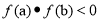 .由
.由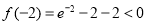 ,
,
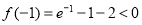 ,
,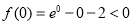 ,
, ,
, ,所以
,所以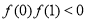 故选C
故选C
考点:函数的零点的判定定理,以及学生的计算能力.

 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案