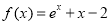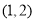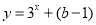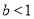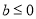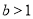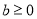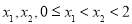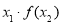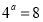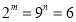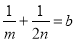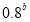题目内容
已知函数
定义在(―1，1)上，对于任意的
，有
，且当
时，
。
(1)验证函数
是否满足这些条件；
(2)判断这样的函数是否具有奇偶性和单调性，并加以证明；
(3)若
，求方程
的解。
（1）详见解析；（2）奇函数，
，证明详见解析；（3）x=
【解析】
试题分析：(1)只要把x、y、
代入函数解析式化简即可得：
，然后验证定义域范围符合即可；
（2）可以根据函数的奇偶性和单调性的定义，并利用赋值法，变量代换的方法得到f(－x)=－f(x)为奇函数和
、
时
为减函数；
（3）利用奇函数和
，得到
和
，代入已知方程即可解决.
试题解析：（1）
∴－1<x<1即定义域为(－1,1)
∴成立
4分
（2）令x=y=0，则f(0)=0，令y=－x则f(x)+f(－x)=0
∴f(－x)=－f(x)为奇函数
任取
、
8分
（3）∵f(x)为奇函数 ∴
由
∵f(x)为(－1，1)上单调函数 
13分
考点：函数性质的综合应用.
练习册系列答案
相关题目
