题目内容
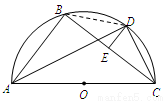
如图所示，AC为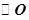
的直径，D为
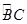的中点，E为BC的中点.
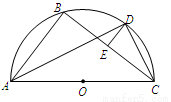
（Ⅰ）求证：AB∥DE；
（Ⅱ）求证：2AD·CD＝AC·BC.
【答案】
（Ⅰ）详见解析；（Ⅱ）详见解析.
【解析】
试题分析：（Ⅰ）通过连接BD，通过证明与同一条直线垂直的两条直线垂直的思路进行证明线线平行；（Ⅱ）通过证明△DAC∽△ECD，
试题解析：（Ⅰ）连接BD，因为D为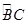
的中点，所以BD＝DC．因为E为BC的中点，所以DE⊥BC．
因为AC为圆的直径，所以∠ABC＝90°，所以AB∥DE． 5分
（Ⅱ）因为D为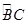的中点，所以∠BAD＝∠DAC，
又∠BAD＝∠DCB，则∠DAC＝∠DCB．
又因为AD⊥DC，DE⊥CE，所以△DAC∽△ECD．
所以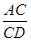
＝
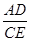，AD·CD＝AC·CE，2AD·CD＝AC·2CE，
因此2AD·CD＝AC·BC． 10分
考点：1.线线平行的证明；2.三角形相似的证明.
练习册系列答案
名校课堂系列答案
相关题目
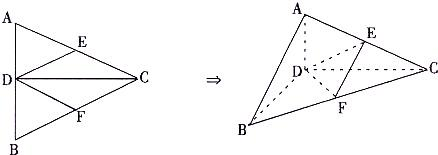
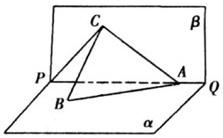如图所示，PQ为平面α、β的交线，已知二面角α-PQ-β为直二面角，A∈PQ，B∈α，C∈β，CA=CB=kAB（k∈R*），∠BAP=45°．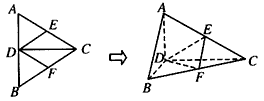
时，求二面角B-AC-P的大小．
