题目内容
如图所示,PQ为平面α、β的交线,已知二面角α-PQ-β为直二面角,A∈PQ,B∈α,C∈β,CA=CB=kAB(k∈R*),∠BAP=45°.(1)证明:BC⊥PQ;
(2)设点C在平面α内的射影为点O,当k取何值时,O在平面ABC内的射影G恰好为△ABC的重心?
(3)当
 时,求二面角B-AC-P的大小.
时,求二面角B-AC-P的大小.
【答案】分析:(1)在平面β内过点C作CE⊥PQ于点E,由题知点E与点A不重合,连接EB.看出点C在平面α内的射影为点E,根据线与线垂直得到线与面垂直,得到结论.
(2)由(1)知,O点即为E点,设点F是O在平面ABC内的射影,连 接BF并延长交AC于点D,由题意可知,若F是△ABC的重心,则点D为AC的中点,根据三垂线定理得到线与线垂直,得到结论.
(3)以O为原点,以OB、OA、OC所在的直线为x轴、y轴、z轴建立空间直角坐标系O-xyz,设出线段的长度,表示出要用的点的坐标,做出两个平面的法向量,根据向量之间的角度来求面与面的夹角.
解答:解: (1)在平面β内过点C作CE⊥PQ于点E,由题知点E与点A不重合,连接EB.
(1)在平面β内过点C作CE⊥PQ于点E,由题知点E与点A不重合,连接EB.
∵α⊥β,α∩β=PQ,∴CE⊥α,即点C在平面α内的射影为点E,
又∵CA=CB,∴EA=EB.∵∠BAE=45°,∴∠ABE=45°,∠AEB=90°,故BE⊥PQ,又∵CE⊥PQ,∴PQ⊥平面EBC,∵BC?平面EBC,故BC⊥PQ.
(2)由(1)知,O点即为E点,设点F是O在平面ABC内的射影,连 接BF并延长交AC于点D,由题意可知,若F是△ABC的重心,则点D为AC的中点.
 ∵BO⊥PQ,平面角α-PQ-β为直二面角,
∵BO⊥PQ,平面角α-PQ-β为直二面角,
∴BO⊥β,∴OB⊥AC,由三垂线定理可知AC⊥BF,即AC⊥BD,∴AB=BC=AC,即k=1;反之,当k=1时,三棱锥O-ABC为正三棱锥,此时,点O在平面ABC内的射影恰好为△ABC的重心.
(3)由(2)知,可以O为原点,以OB、OA、OC所在的直线为x轴、y轴、z轴建立空间直角坐标系O-xyz(如图所示)
不妨设 ,在Rt△OAB中,∠ABO=∠BAO=45°,所以BO=AO=
,在Rt△OAB中,∠ABO=∠BAO=45°,所以BO=AO= ,由CA=CB=kAB且
,由CA=CB=kAB且 得,AC=2,∴OC=1,则
得,AC=2,∴OC=1,则 .
.
所以
设n1(x,y,z)是平面ABC的一个法向量,由 得
得
取x=1,得
易知n2=(1,0,0)是平面β的一个法向量,
设二面角B-AC-P的平面角为θ,所以 ,由图可知,
,由图可知,
二面角B-AC-P的大小为 .
.
点评:本题看出线面之间的关系和用向量来求两个平面的夹角的问题,把向量利用到立体几何中,降低了题目的难度,本题是近几年高考必考的题型
(2)由(1)知,O点即为E点,设点F是O在平面ABC内的射影,连 接BF并延长交AC于点D,由题意可知,若F是△ABC的重心,则点D为AC的中点,根据三垂线定理得到线与线垂直,得到结论.
(3)以O为原点,以OB、OA、OC所在的直线为x轴、y轴、z轴建立空间直角坐标系O-xyz,设出线段的长度,表示出要用的点的坐标,做出两个平面的法向量,根据向量之间的角度来求面与面的夹角.
解答:解:
 (1)在平面β内过点C作CE⊥PQ于点E,由题知点E与点A不重合,连接EB.
(1)在平面β内过点C作CE⊥PQ于点E,由题知点E与点A不重合,连接EB.∵α⊥β,α∩β=PQ,∴CE⊥α,即点C在平面α内的射影为点E,
又∵CA=CB,∴EA=EB.∵∠BAE=45°,∴∠ABE=45°,∠AEB=90°,故BE⊥PQ,又∵CE⊥PQ,∴PQ⊥平面EBC,∵BC?平面EBC,故BC⊥PQ.
(2)由(1)知,O点即为E点,设点F是O在平面ABC内的射影,连 接BF并延长交AC于点D,由题意可知,若F是△ABC的重心,则点D为AC的中点.
 ∵BO⊥PQ,平面角α-PQ-β为直二面角,
∵BO⊥PQ,平面角α-PQ-β为直二面角,∴BO⊥β,∴OB⊥AC,由三垂线定理可知AC⊥BF,即AC⊥BD,∴AB=BC=AC,即k=1;反之,当k=1时,三棱锥O-ABC为正三棱锥,此时,点O在平面ABC内的射影恰好为△ABC的重心.
(3)由(2)知,可以O为原点,以OB、OA、OC所在的直线为x轴、y轴、z轴建立空间直角坐标系O-xyz(如图所示)
不妨设
 ,在Rt△OAB中,∠ABO=∠BAO=45°,所以BO=AO=
,在Rt△OAB中,∠ABO=∠BAO=45°,所以BO=AO= ,由CA=CB=kAB且
,由CA=CB=kAB且 得,AC=2,∴OC=1,则
得,AC=2,∴OC=1,则 .
.所以

设n1(x,y,z)是平面ABC的一个法向量,由
 得
得
取x=1,得

易知n2=(1,0,0)是平面β的一个法向量,
设二面角B-AC-P的平面角为θ,所以
 ,由图可知,
,由图可知,二面角B-AC-P的大小为
 .
.点评:本题看出线面之间的关系和用向量来求两个平面的夹角的问题,把向量利用到立体几何中,降低了题目的难度,本题是近几年高考必考的题型

练习册系列答案
相关题目
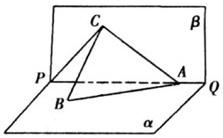 如图所示,PQ为平面α、β的交线,已知二面角α-PQ-β为直二面角,A∈PQ,B∈α,C∈β,CA=CB=kAB(k∈R*),∠BAP=45°.
如图所示,PQ为平面α、β的交线,已知二面角α-PQ-β为直二面角,A∈PQ,B∈α,C∈β,CA=CB=kAB(k∈R*),∠BAP=45°.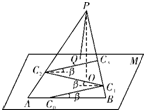 (2012•蓝山县模拟)某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与山脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=
(2012•蓝山县模拟)某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与山脚所在水平面M所成的二面角为α(0°<α<90°),且sinα= α,KL
α,KL
