题目内容
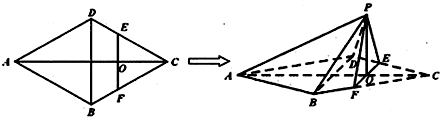
如图,在边长为4的菱形ABCD中,∠DAB=60°.点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O.沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.
(Ⅰ)求证:BD⊥平面POA;
(Ⅱ)记三棱锥P- ABD体积为V1,四棱锥P—BDEF体积为V2.求当PB取得最小值时的V1:V2值.

【答案】
(Ⅰ)证明:在菱形 中,∵
中,∵ 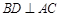 ,∴
,∴ 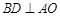 .1分
.1分
∵ 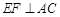 ,∴
,∴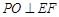 ,
,
∵ 平面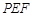 ⊥平面
⊥平面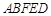 ,平面
,平面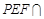 平面
平面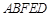
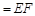 ,且
,且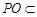 平面
平面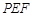 ,
,
∴ 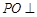 平面
平面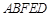 , 2分
, 2分
∵ 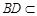 平面
平面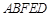 ,∴
,∴ 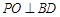 .3分
.3分
∵ 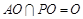 ,所以
,所以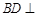 平面
平面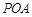 .4分
.4分
(Ⅱ)连结 ,设
,设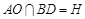 .
.
由(Ⅰ)知,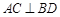 .∵
.∵ 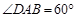 ,
,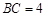 ,
,
∴ 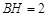 ,
,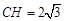 .5分设
.5分设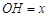 (
(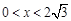 ).
).
由(Ⅰ)知,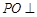 平面
平面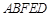 ,故
,故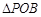 为直角三角形.
为直角三角形.
∴ 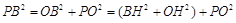 ,
,
∴ 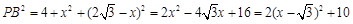 7分
7分
当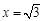 时,
时,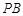 取得最小值,此时
取得最小值,此时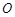 为
为 中点.8分
中点.8分
∴  ,9分
,9分
∴  ,10分
,10分
∴ 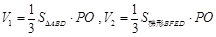 . 11分
. 11分
∴  .
.
∴ 当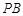 取得最小值时,
取得最小值时,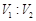 的值为
的值为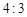 .
.
【解析】略

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
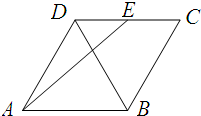 如图,在边长为4的菱形ABCD中,∠BAD=60°,E为CD的中点,则
如图,在边长为4的菱形ABCD中,∠BAD=60°,E为CD的中点,则