题目内容

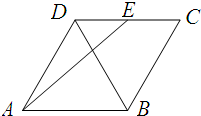如图，在边长为4的菱形ABCD中，∠BAD=60°，E为CD的中点，则
AE
•
BD
的值为
4
4
．
分析：利用向量的基本定理，结合数量积的定义进行求解．
解答：解：∵E为CD的中点，∴
AE
=
AD
+
DE
=
AD
+
1
2
DE
=
AD
+
1
2
AB
，
BD
=
AD
-
AB
，
∴
AE
•
BD
=(
AD
+
1
2
AB
)?(
AD
-
AB
)=
AD
2-
1
2
AB
2-
1
2
AD
?
AB
，
∵边长为4的菱形ABCD中，∠BAD=60°，
∴
AD
?
AB
=|
AD|
?|
AB|
cos?600=4×4×
1
2
=8，
∴
AE
•
BD
=42-
1
2
×42-
1
2
×8=16-8-4=4．
故答案为：4．
点评：本题主要考查平面向量的基本定理的应用，以及平面向量的数量积公式的应用．
练习册系列答案
相关题目
（2012•福州模拟）如图，在边长为4的菱形ABCD中，∠DAB=60°．点E、F分别在边CD、CB上，点E与点C、D不重合，EF⊥AC，EF∩AC=O．沿EF将△CEF翻折到△PEF的位置，使平面PEF⊥平面ABFED．
（Ⅰ）求证：BD⊥平面POA；
（Ⅱ）记三棱锥P-ABD体积为V1，四棱锥P-BDEF体积为V2．求当PB取得最小值时的V1：V2值．
（2013•茂名二模）如图，在边长为4的菱形ABCD中，∠DAB=60°，点E，F分别在边CD，CB上，点E与点C，点D不重合，EF⊥AC，EF∩AC=O，沿EF将△CEF折起到△PEF的位置，使得平面PEF⊥平面ABFED

（1）求证：BD⊥平面POA
（2）当点O 在何位置时，PB取得最小值？
（3）当PB取得最小值时，求四棱锥P-BDEF的体积．
（2012•茂名二模）如图，在边长为4的菱形ABCD中，∠DAB=60°，点E，F分别在边CD，CB上，点E与点C，点D不重合，EF⊥AC，EF∩AC=O，沿EF将△CEF折起到△PEF的位置，使得平面PEF⊥平面ABFED
（1）求证：BD⊥平面POA
（2）设AO∩BD=H，当O为CH中点时，若点Q满足
AQ
=
QP
，求直线OQ与平面PBD所成角的正弦值．
（2012•汕头二模）如图，在边长为4的菱形ABCD中，∠DAB=60°．点E、F分别在边CD、CB上，点E与点C、D不重合，EF⊥AC，EF∩AC=O，沿EF将△CEF翻折到△PEF的位置，使平面PEF⊥平面ABEFD．
（1）求证：BD⊥平面POA；
（2）记三棱锥P-ABD体积为V1，四棱锥P-BDEF体积为V2，且
V1
V2
=
4
3
，求此时线段PO的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网