题目内容
在区间【- ,
, 】内随机取两个数分别记作a,b。则使得函数
】内随机取两个数分别记作a,b。则使得函数 =
=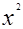 +
+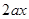 -
- +
+ 有零点的概率为 ( )
有零点的概率为 ( )
A. | B. | C.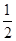 | D. |
B
解析试题分析:先判断概率的类型,由题意知本题是一个几何概型,由a,b使得函数f(x)=x2+2ax-b2+π有零点,得到关于a、b的关系式,写出试验发生时包含的所有事件和满足条件的事件,做出对应的面积,求比值得到结果.解:由题意知本题是一个几何概型,∵a,b使得函数f(x)=x2+2ax-b2+π有零点,∴△≥0,∴a2+b2≥π,试验发生时包含的所有事件是Ω={(a,b)|-π≤a≤π,-π≤b≤π}∴S=(2π)2=4π2,而满足条件的事件是{(a,b)|a2+b2≥π},∴s=4π2-π2=3π2,由几何概型公式得到P= 故选B.
故选B.
考点:几何概型
点评:高中必修中学习了几何概型和古典概型两种概率问题,先要判断该概率模型是不是古典概型,再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.再看是不是几何概型,它的结果要通过长度、面积或体积之比来得到.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在平面区域 内任意取一点
内任意取一点 内的概率是( )
内的概率是( )
A. | B. | C. | D. |
从只含有二件次品的10个产品中取出三件,设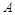 为“三件产品全不是次品”,
为“三件产品全不是次品”,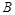 为“三件产品全是次品”,
为“三件产品全是次品”,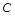 为“三件产品不全是次品”,则下列结论正确的是:
为“三件产品不全是次品”,则下列结论正确的是:
A.事件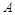 与 与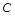 互斥 互斥 | B.事件C是随机事件 |
| C.任两个均互斥 | D.事件B是不可能事件 |
设函数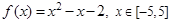 .若从区间
.若从区间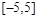 内随机选取一个实数
内随机选取一个实数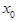 ,则所选取的实数
,则所选取的实数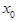 满足
满足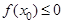 的概率为( )
的概率为( )
A.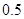 | B.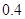 | C.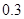 | D.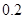 |
已知正三棱锥 的底面边长为
的底面边长为 ,高为
,高为 ,在正三棱锥内任取一点
,在正三棱锥内任取一点 ,使得
,使得 的概率为( )
的概率为( )
A. | B. | C. | D. |





 满足约束条件
满足约束条件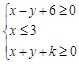 ,且
,且 的最小值为6.若实数
的最小值为6.若实数 则点
则点 落在上述区域内的概率为( )
落在上述区域内的概率为( )



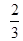 ,则阴影区域的面积为( )
,则阴影区域的面积为( ) 


