题目内容
已知向量a=(cos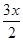 ,sin
,sin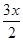 ),b=(cos
),b=(cos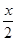 ,-sin
,-sin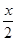 ),且x∈[0,
),且x∈[0,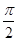 ],
],
(1)求a·b; (2)求 |a+b|;
(3)求函数f(x)=a·b-|a+b|的最小值及此时的x值.
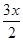 ,sin
,sin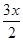 ),b=(cos
),b=(cos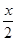 ,-sin
,-sin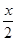 ),且x∈[0,
),且x∈[0,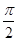 ],
],(1)求a·b; (2)求 |a+b|;
(3)求函数f(x)=a·b-|a+b|的最小值及此时的x值.

本试题主要考查了向量的数量积的运算以及向量与三角函数性质的结合求解最值的综合运用。
(1)第一问直接利用数量积公式求解,结合三角函数中两角和差的公式得到结论。
(2)结合二倍角公式表示模的平方就是向量的平方得到。
(3)根据函数关系式,然后变形为形如二次函数的函数,得到函数的最值
(1)第一问直接利用数量积公式求解,结合三角函数中两角和差的公式得到结论。
(2)结合二倍角公式表示模的平方就是向量的平方得到。
(3)根据函数关系式,然后变形为形如二次函数的函数,得到函数的最值

练习册系列答案
相关题目
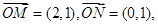 O为坐标原点,动点
O为坐标原点,动点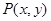 满足
满足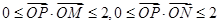 ,则
,则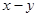 的最小值是
的最小值是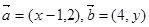 ,若
,若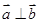 ,则16x+4y的最小值为____ ____。
,则16x+4y的最小值为____ ____。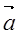 =(1,2),
=(1,2),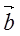 =(x,1),若
=(x,1),若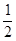
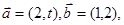 若
若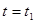 时,
时,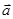 ∥
∥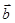 ;
;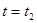 时,
时,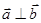 ,则 ( )
,则 ( )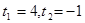
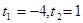

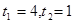
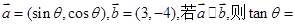
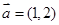 ,
,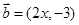 ,若
,若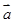 ∥
∥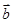 ,则
,则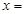 ( )
( )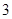
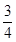
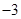
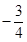
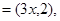 b=(6,1),若a∥b,则
b=(6,1),若a∥b,则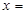 ( )
( )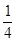

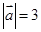 ,
,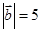 ,若
,若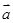 //
//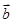 ,则
,则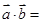 .
.