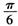题目内容
如图,三棱锥S-ABC 中,SC丄底面ABC,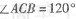 ,SC=AC=BC=
,SC=AC=BC=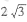 ,M为SB中点,N在AB上,满足MN 丄 BC.
,M为SB中点,N在AB上,满足MN 丄 BC.
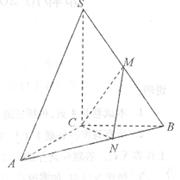
(I)求点N到平面SBC的距离;
(II)求二面角C-MN-B的大小.
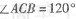 ,SC=AC=BC=
,SC=AC=BC=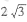 ,M为SB中点,N在AB上,满足MN 丄 BC.
,M为SB中点,N在AB上,满足MN 丄 BC.
(I)求点N到平面SBC的距离;
(II)求二面角C-MN-B的大小.
解:(1)取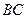 的中点
的中点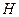 ,连结
,连结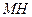 、
、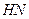 ,则由
,则由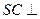 底面
底面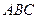 ,
,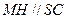 ,
,

知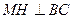 ,又
,又 ,∴
,∴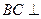 平面
平面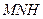 ,
,
∴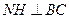 ,∴
,∴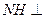 平面SBC,∴
平面SBC,∴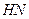 即为点N到平面SBC的距离.
即为点N到平面SBC的距离.
由题易知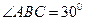 ,所以
,所以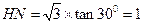 .…………5分
.…………5分
(2)(方法一)在直角三角形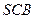 中,
中, 因为
因为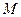 为
为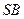 的中点,所以
的中点,所以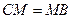 。由(1)知
。由(1)知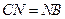 ,所以
,所以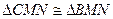 ,作
,作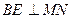 于点
于点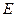 ,连结
,连结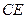 ,则
,则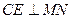 ,所
,所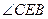 为二面角
为二面角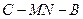 的平面角.
的平面角.
在三角形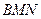 中,易知
中,易知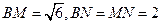 ,故可求
,故可求 ,所以
,所以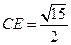 ,在
,在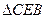 中,由余弦定理可得
中,由余弦定理可得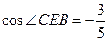 ,所以
,所以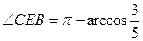 ,即二面角
,即二面角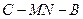 的大小为
的大小为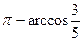 . …………12分
. …………12分
(方法二)过C作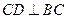 交AB于D,如图建立空间直角坐标系,则易知点
交AB于D,如图建立空间直角坐标系,则易知点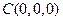 、
、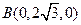 、
、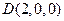 、
、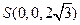 、
、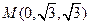 、
、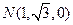 ,则
,则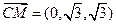 、
、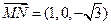 、
、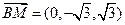 ,
,
设平面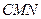 的法向量为
的法向量为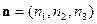 ,则由
,则由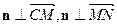 ,得
,得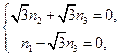 故可取
故可取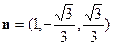 ,
,
再设平面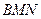 的法向量为
的法向量为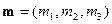 ,则由
,则由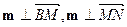 ,得
,得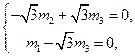 故可取
故可取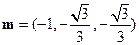 ,则向量
,则向量 与
与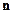 的夹角大小即为二面角
的夹角大小即为二面角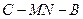 的大小。
的大小。
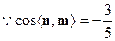 ,故二面角
,故二面角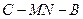 的大小
的大小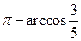 所求. …………12分
所求. …………12分
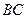 的中点
的中点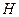 ,连结
,连结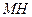 、
、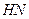 ,则由
,则由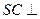 底面
底面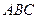 ,
,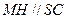 ,
,
知
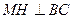 ,又
,又 ,∴
,∴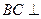 平面
平面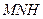 ,
,∴
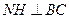 ,∴
,∴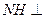 平面SBC,∴
平面SBC,∴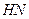 即为点N到平面SBC的距离.
即为点N到平面SBC的距离.由题易知
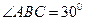 ,所以
,所以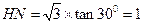 .…………5分
.…………5分(2)(方法一)在直角三角形
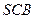 中,
中, 因为
因为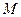 为
为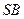 的中点,所以
的中点,所以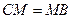 。由(1)知
。由(1)知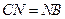 ,所以
,所以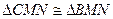 ,作
,作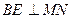 于点
于点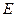 ,连结
,连结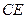 ,则
,则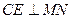 ,所
,所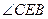 为二面角
为二面角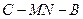 的平面角.
的平面角.在三角形
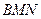 中,易知
中,易知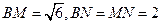 ,故可求
,故可求 ,所以
,所以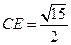 ,在
,在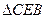 中,由余弦定理可得
中,由余弦定理可得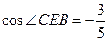 ,所以
,所以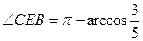 ,即二面角
,即二面角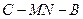 的大小为
的大小为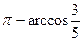 . …………12分
. …………12分(方法二)过C作
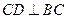 交AB于D,如图建立空间直角坐标系,则易知点
交AB于D,如图建立空间直角坐标系,则易知点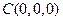 、
、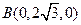 、
、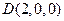 、
、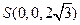 、
、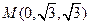 、
、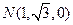 ,则
,则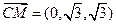 、
、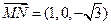 、
、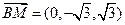 ,
, 设平面
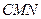 的法向量为
的法向量为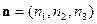 ,则由
,则由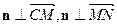 ,得
,得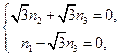 故可取
故可取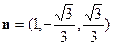 ,
,再设平面
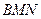 的法向量为
的法向量为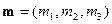 ,则由
,则由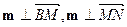 ,得
,得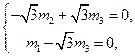 故可取
故可取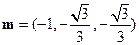 ,则向量
,则向量 与
与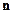 的夹角大小即为二面角
的夹角大小即为二面角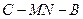 的大小。
的大小。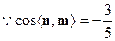 ,故二面角
,故二面角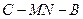 的大小
的大小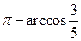 所求. …………12分
所求. …………12分略

练习册系列答案
相关题目
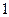 的正方体
的正方体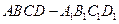 中,
中,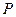 为线段
为线段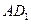 上的点,且满足
上的点,且满足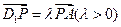 .
.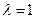 时,求证:平面
时,求证:平面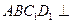 平面
平面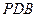 ;
;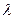 为何值,三棱锥
为何值,三棱锥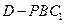 的体积
的体积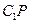 与
与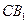 所成的角的余弦值.
所成的角的余弦值.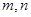 为直线,
为直线,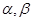 为平面,给出下列命题:
为平面,给出下列命题: ②
②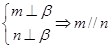 ③
③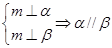 ④
④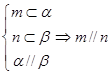
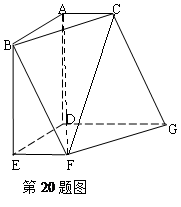
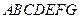 中,平面
中,平面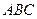 ∥平面
∥平面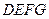 ,
,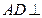 平面
平面 ,
,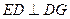 ,
,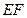 ∥
∥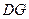 ,且
,且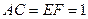 ,
,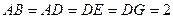 .
.
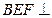 平面
平面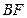 ∥平面
∥平面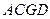 ;
;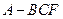 的体积.
的体积. .
.
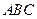 的边长为4,
的边长为4,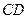 是
是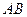 边上的高,
边上的高,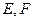 分别是
分别是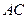 和
和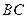 边的中点,现将△
边的中点,现将△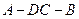 .
.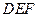 的位置关系,并
的位置关系,并 说明理由;
说明理由;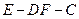 的余弦值;
的余弦值;
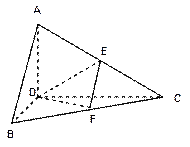
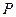 ,使
,使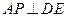 ?证明你的结论.
?证明你的结论. 
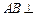 面
面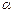 ,
,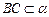 ,
,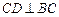 ,
,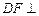 面
面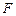 ,
,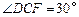 ,且
,且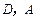 在平面
在平面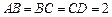 ,则
,则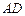 的长为
的长为 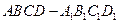 中,异面直线
中,异面直线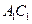 与
与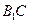 的夹角的大小为__________
的夹角的大小为__________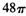 的球面上三点,且A
的球面上三点,且A B=2,BC=4,
B=2,BC=4,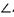 ABC=
ABC=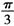 为球心,则二面角0-AB-C的大小为( )
为球心,则二面角0-AB-C的大小为( )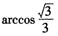 B.
B.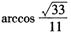 C.
C.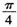 D.
D.