题目内容
4.若数列{an}满足a1=1,an-1+an=$\frac{{a}_{n}{a}_{n-1}}{({n}^{2}-n)(-1)^{n}}$(n∈N,且n≥2),则数列{$\frac{{a}_{n+1}}{(2n+1)(2n+3)}$}的前6项和为( )| A. | -3 | B. | -$\frac{1}{15}$ | C. | $\frac{1}{15}$ | D. | 3 |
分析 an-1+an=$\frac{{a}_{n}{a}_{n-1}}{({n}^{2}-n)(-1)^{n}}$(n∈N,且n≥2),变形为(-1)n($\frac{1}{{a}_{n}}+\frac{1}{{a}_{n-1}}$)=$\frac{1}{n-1}-\frac{1}{n}$,利用“裂项求和”可得:$\frac{1}{{a}_{1}}+(-1)^{n}\frac{1}{{a}_{n}}$=1-$\frac{1}{n}$.对n分类讨论可得:an=(-1)n+1n.于是$\frac{{a}_{n+1}}{(2n+1)(2n+3)}$=$\frac{(-1)^{n}(n+1)}{(2n+1)(2n+3)}$=$(-1)^{n}\frac{1}{4}(\frac{1}{2n+1}+\frac{1}{2n+3})$.即可得出.
解答 解:∵an-1+an=$\frac{{a}_{n}{a}_{n-1}}{({n}^{2}-n)(-1)^{n}}$(n∈N,且n≥2),
∴(-1)n($\frac{1}{{a}_{n}}+\frac{1}{{a}_{n-1}}$)=$\frac{1}{n-1}-\frac{1}{n}$,
∴$(\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}})$-$(\frac{1}{{a}_{2}}+\frac{1}{{a}_{3}})$+$(\frac{1}{{a}_{3}}+\frac{1}{{a}_{4}})$-…+(-1)n$(\frac{1}{{a}_{n-1}}+\frac{1}{{a}_{n}})$=$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n-1}-\frac{1}{n})$=1-$\frac{1}{n}$.
当n为奇数时,$\frac{1}{{a}_{1}}-\frac{1}{{a}_{n}}$=$1-\frac{1}{n}$,
∴an=n.
当n为偶数时,$\frac{1}{{a}_{1}}+\frac{1}{{a}_{n}}$=1-$\frac{1}{n}$,解得an=-n.
∴an=(-1)n+1n.
∴$\frac{{a}_{n+1}}{(2n+1)(2n+3)}$=$\frac{(-1)^{n}(n+1)}{(2n+1)(2n+3)}$=$(-1)^{n}\frac{1}{4}(\frac{1}{2n+1}+\frac{1}{2n+3})$.
∴数列{$\frac{{a}_{n+1}}{(2n+1)(2n+3)}$}的前6项和=$\frac{1}{4}[-(\frac{1}{3}+\frac{1}{5})+(\frac{1}{5}+\frac{1}{7})$-…+$(\frac{1}{13}+\frac{1}{15})]$
=$\frac{1}{4}$$(\frac{1}{15}-\frac{1}{3})$
=-$\frac{1}{15}$.
故选:B.
点评 本题考查了“裂项求和”方法,考查了变形能力,考查了分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案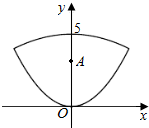 已知抛物线y=$\frac{1}{4}{x}^{2}$和y=-$\frac{1}{16}$x2+5所围成的封闭曲线如图所示,给定点 A(0,a),若在此封闭曲线上恰有三对不同的点,满足每一对点关于点A 对称,则实数a的取值范围是( )
已知抛物线y=$\frac{1}{4}{x}^{2}$和y=-$\frac{1}{16}$x2+5所围成的封闭曲线如图所示,给定点 A(0,a),若在此封闭曲线上恰有三对不同的点,满足每一对点关于点A 对称,则实数a的取值范围是( )| A. | (1,3) | B. | (2,4) | C. | ($\frac{3}{2}$,3) | D. | ($\frac{5}{2}$,4) |
| A. | 2015×1010 | B. | 2015×1011 | C. | 2016×1010 | D. | 2016×1011 |
| A. | $\frac{32}{9}$ | B. | 4-ln3 | C. | 4+ln3 | D. | 2-ln3 |
| A. | 10 | B. | 100 | C. | $\sqrt{10}$ | D. | 10${\;}^{\frac{1}{4}}$ |
 据统计某校学生在上学路上所需时间最多不超过120分钟.该校随机抽取部分新入校的新生其在上学路上所需时间(单位:分钟)进行调查,并将所得数据绘制成频率分布直方图.
据统计某校学生在上学路上所需时间最多不超过120分钟.该校随机抽取部分新入校的新生其在上学路上所需时间(单位:分钟)进行调查,并将所得数据绘制成频率分布直方图.